Каждый химический элемент имеет набор изотопов (ядра атомов отличаются количеством частиц - нейтронов). Например водород имеет распрастранённых три изотопа:
H - протий (в ядре 1 - протон и 0 нейтронов)
D - дейтерий (в ядре 1 протон и 1 нейтрон)
T - тритий (в ядре 1 протон и 2 нейтрона) - радиоактивный
Но в природе они встречаются с разной частотой. Около 90% - первый, второй - реже , третий - ещё реже (проценты можешь посмотреть в инете)
Указанная атомная масса в ячейке - это среднестатистическое значение массы, т.е с учётом %-го существования в природе.
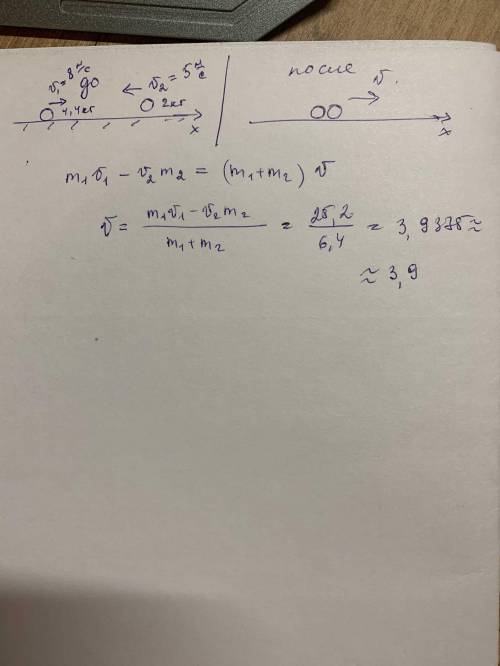
Объяснение:Два пластилиновых шарика массами m1= 4,4 кг и m2= 2 кг движутся по гладкой горизонтальной поверхности вдоль одной прямой навстречу друг другу со скоростями v1= 8 м/с и v2= 5 м/с соответственно. Через некоторое время шарики сталкиваются, склеиваются и далее начинают двигаться как одно тело. Определи скорость шариков после склеивания. (ответы округли до десятых.) Шаг 1. Найди импульс первого шарика до взаимодействия: p1= 4,4*8 кг·м/с=35,2кг·м/с. Шаг 2. Найди импульс второго шарика до взаимодействия: p2= 2*5 кг·м/с=10кг·м/с. Шаг 3. Найди суммарный импульс двух шариков до взаимодействия, учитывая, что шарики движутся навстречу друг другу: p= 35,2кг·м/с-10кг·м/с=25,2 кг·м/с.
Шаг 4. Найди массу тела, которое получается из слипшихся шариков: m= 6,4кг. Шаг 5. Обозначив скорость тела после слипания шариков как v, запиши импульс P тела после взаимодействия: (m1+m2)V=p1⋅p2 Шаг 6. Поскольку два шарика являются замкнутой системой, то для них выполняется закон сохранения импульса: импульс системы до взаимодействия равен импульсу системы после взаимодействия. Составь уравнение согласно закону сохранения импульса: (m1+m2)V=p1⋅p2 — и реши его относительно v с точностью до десятых: v = 3,9м/с.
Вес детали в воде равен силе тяжести, действующей на эту деталь и силе архимеда.
F(архимеда) = V(тела)*Po(воды)*g
F(тяжести) = mg = Po(тела)*V(тела)*g
F(архимеда) < F(тяжести), ведь тело тонет (его плотность больше плотности воды)
P(в воде) = F(тяжести) - F(архимеда)
Дальше подставляй числа