уравнение Менделеева-Клапейрона

из этого же уравнения выводятся несколько других
Закон Шарля (описывает изохорный процесс)
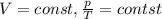
Закон Гей-Люссака (описывает изобарный процесс)
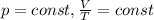
и Закон Бойля-Мариотта (описывает изотермический процесс)

их названия, конечно, знать вовсе не обезательно, и воводятся они из первого уравнения довольно легко.
также внутрянняя энергия идеального газа
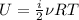
где i - количество степеней свободы (для одноатомного газа 3, для двухатомного 5)
работа идеального газа
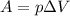
Также первый закон термодинамики
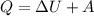
Q - кол-во теплоты, U - внутр. энергия, A - соверш. работа.
уравнение Менделеева-Клапейрона

из этого же уравнения выводятся несколько других
Закон Шарля (описывает изохорный процесс)
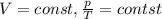
Закон Гей-Люссака (описывает изобарный процесс)
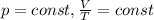
и Закон Бойля-Мариотта (описывает изотермический процесс)

их названия, конечно, знать вовсе не обезательно, и воводятся они из первого уравнения довольно легко.
также внутрянняя энергия идеального газа
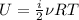
где i - количество степеней свободы (для одноатомного газа 3, для двухатомного 5)
работа идеального газа
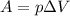
Также первый закон термодинамики
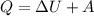
Q - кол-во теплоты, U - внутр. энергия, A - соверш. работа.
Дослідження залежності ККД від кута нахилу похилої площини
Мета: Встановити експериментально залежність ККД від кута нахилу похилої площини до горизонту; порівняти результати експериментально одержаної залежності та теоретично отриманого співвідношення.
Обладнання: Похила площина, динамометр, вимірювальна стрічка або лінійка, брусок, транспортир.
Теоретичні відомості
ККД похилої площини є відношення корисної роботи до затраченої , тобто:
; , (1)
де – маса тіла;
– висота похилої площини;
– прискорення вільного падіння;
– сила, необхідна для рівномірного руху тіла вгору по похилій площині;
– довжина похилої площини.
З малюнка
, (2)
де – коефіцієнт тертя;
– кут нахилу похилої площини.
Підставивши (1) в (2) одержимо:
(3)
Щоб знайти коефіцієнт тертя , розмістимо брусок на похилій площині і піднімаючи її за один кінець знайдемо граничний кут, при якому брусок буде ковзати в низ. Це станеться тоді, коли скочуюча сила , звідки:
.
Тоді формула (3) набуває вигляду:
Объяснение: