Решение. В проекциях на горизонтальную ось формула для ускорения имеет вид:
Отсюда
Проекция перемещения на горизонтальную ось при равноускоренном прямолинейном движении имеет вид:
Определим значения искомых величин:
м/с
м
ответ: 10 м/с; 125 м
Задание 4
Дано:
мин
Найти:
Решение. Первое тело движется равноускоренно с ускорением м/с² с начальной координатой м. Второе тело движется равномерно прямолинейно с начальной скоростью м/с с начальной координатой
Для того чтобы определить время встречи, следует приравнять соответствующие координаты материальных точек:
— не удовлетворяет смыслу задачи
Таким образом, материальные точки встретятся через .
Место встречи: подставим значение в любую из координат:
м
Определим координаты положения для каждой материальной точки за :
Расстоянием между материальными точками будет модуль разности соответствующих координат:
Закон Кулона F = kQq/R², в форме, сформулированный в элементарной электростатике – имеет фундаментальный универсальный смысл и остаётся верен и в случае физики Эйнштейна, если движение зарядов перпендикулярно линии взаимодействия, поскольку связывает независящие от системы отсчёта величины: силу, заряды и поперечное расстояние. Правда, формула F = kQq/R² в этом случае – это не сила Кулона, а суммарная сила взаимодействия двух зарядов, включающая в себя нечто большее.
Сила взаимодействия двух зарядов kQq/R², перпендикулярно соединяющей их линии останется точно такой же и в случае их движения, или движения одного из них поперёк соединяющей их линии. Тем не менее, в случае взаимодействия не просто одиночных зарядов, а потоков подвижных зарядов (электротоков), когда сила воздействия одного потока заряженных частиц на элементы параллельного – складывается, как суперпозиция отдельных сил Кулона – всё усложняется тем, что продольные расстояния при относительном движении сжимаются, и силы относительно-подвижных взаимодействий становятся больше сил относительно-неподвижных взаимодействий. Причём, оказывается, что силы Кулона зависят от относительной скорости движения квадратично.
Если, скажем, токи одной природы (например, электронные) однонаправленные, то силы Кулона относительно подвижных элементов [ep] – это силы притяжения, и они сильнее, а силы Кулона относительно неподвижных элементов [ee]/[pp] – это силы отталкивания, и они слабее. Возникает притяжение.
Если, скажем, токи разной природы (электронный и положительно-ионный) однонаправленные (т.е. математически разнонаправленные токи), то силы Кулона относительно подвижных элементов [ee]/[pp] – это силы отталкивания, и они сильнее, а силы Кулона относительно неподвижных элементов [ep] – это силы притяжения, и они слабее. Возникает отталкивание.
Если, токи одной природы разнонаправленные, то силы Кулона относительно подвижных элементов [ep] – это силы притяжения, и они умеренные, а силы Кулона относительно сильно-подвижных элементов [ee]/[pp] – это силы отталкивания, и они квадратично большие. Возникает отталкивание. Четвёртый вариант нетрудно разобрать самостоятельно.
В итоге, получается, что два однонаправленных тока (уже с учётом и природы и направления потоков) начинают притягиваться, а два разнонаправленных тока – отталкиваться. При математическом обобщении (интегрировании) всех отличий относительно-подвижных сил Кулона от относительно-неподвижных сил Кулона – выясняется, что общая сила притяжения однонаправленных токов выражается так, как будто между каждыми двумя отдельными зарядами возникает взаимодействие, описываемое той же формулой, как и сила Кулона, но с добавочным коэффициентом пропорциональности:
F = k(QV/c)(qv/c)/R² , где V/c – приведённая скорость первого тока, а v/c – приведённая скорость второго тока.
Таким образом, оказывается удобным ввести отдельный термин и отдельно учитывать часть поля подвижных заряженных частиц. Этот кусочек (слагаемое) взаимодействия называют магнетизмом и магнитным слагаемым в законе взаимодействия. И этот факт – превосходное доказательство теории относительности Эйнштейна.
Между двумя зарядами, расположенными на линии перпендикулярной их движению возникает сила, которую можно записать так:
F = kQq/R² = [1+Vv/c²]kQq/R² – [Vv/c²]kQq/R² ;
где договорились называть:
F = [1+Vv/c²] kQq/R² – силой Кулона (положительное направление – отталкивание), а
F = –k/c² [VQ][vq]/R² – силой Магнитного взаимодействия Био-Савара-Лапласа (знак минус – притяжение).
Выражение закона Био-Савара-Лапласа здесь показано в элементарной форме, когда линия взаимодействия зарядов перпендикулярна скоростям движения зарядов.
*** [ограничивают зачем-то 5000 символов, поэтому – читаем слудующее решение]
Задание 3
Дано:
Найти: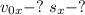
Решение. В проекциях на горизонтальную ось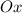 формула для ускорения имеет вид:
формула для ускорения имеет вид:
Отсюда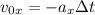
Проекция перемещения на горизонтальную ось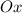 при равноускоренном прямолинейном движении имеет вид:
при равноускоренном прямолинейном движении имеет вид: 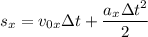
Определим значения искомых величин:
ответ: 10 м/с; 125 м
Задание 4
Дано:
Найти: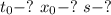
Решение. Первое тело движется равноускоренно с ускорением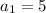 м/с² с начальной координатой
м/с² с начальной координатой 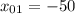 м. Второе тело движется равномерно прямолинейно с начальной скоростью
м. Второе тело движется равномерно прямолинейно с начальной скоростью 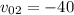 м/с с начальной координатой
м/с с начальной координатой 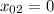
Для того чтобы определить время встречи, следует приравнять соответствующие координаты материальных точек:
Таким образом, материальные точки встретятся через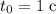 .
.
Место встречи: подставим значение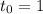 в любую из координат:
в любую из координат:
Определим координаты положения для каждой материальной точки за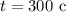 :
:
Расстоянием между материальными точками будет модуль разности соответствующих координат:
ответ: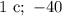 м;
м; 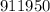 м
м