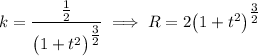Объяснение:
Дано:
x = 2·t
y = t²
R - ?
1)
Находим проекции скоростей:
Vₓ = x' = (2·t)' = 2
Vy = y' = (t²)' = 2·t
Тогда:
V = √ (Vₓ² + Vy²) = √ (2² + (2·t)²) = √ (4 + 4·t²) = 2·√(1 + t²)
Тангенциальное ускорение:
aτ = (V)' = (2·√(1 + t²))' = 2·t / √(1+t²)
2)
Находим полное ускорение:
aₓ = (Vₓ)' = (2)' = 0
ay = (Vy)' = (2·t)' = 2
a = √ (ax² + ay²) = √ (0² + 2²) = 2
3)
Нормальное ускорение:
aₙ = √ (a² - aτ²) = √ ( 4 - 4·t² /(1 + t²))
4)
Радиус кривизны:
R = V² / aₙ = (2·√(1 + t²))² / √ ( 4 - 4·t² /(1 + t²)) =
= 4·(1+t²) ·√ (1+t²) / 2 = 2·(1+t²) √(1+ t²) = 2 · (1 + t²)^(3/2)
При движении по кривой ускорение материальной точки складывается из нормальной составляющей и тангенциальной (причем они ортогональны):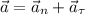
Найдём модули всех указанных векторов.
1)
2)
, где 
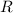- радиус кривизны в данной точке (момент времени). Причём, 
. Таким образом, 
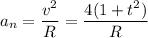
3)
Поскольку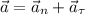
и 
, то из прямоугольного треугольника на трёх указанных векторах получим:
ответ.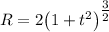
PS. Наиболее быстро ответ можно получить с дифференциальной геометрии.
Кривизной траектории выраженной явно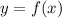
называется величина 
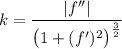, а радиусом кривизны - величина 
.
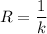Для нашей задачи,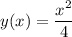
. Отсюда 
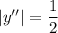и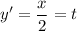 
.
Сразу же получаем