( )
1. В состоянии теплового равновесия находятся
А пловец и вода в бассейне
Б включенная лампа накаливания и воздух в комнате
В воздух внутри холодильника и продукты в нем
Г оконное стекло и воздух в комнате в зимний мороз
2. При теплопередаче энергия переходит
А от Земли к Солнцу
Б от человека к окружающему воздуху в холодный день
В от воздуха в комнате к кипящей воде в кастрюле
Г от снега, принесенного в теплую комнату, к воздуху в комнате
3. Действие жидкостного термометра основано на явлении
А сохранения объема жидкости
Б превращения жидкости в пар
В теплового расширения
Г диффузии в жидкости
4. Явление, благодаря которому дым из печи устремляется в трубу, а не в комнату называется
А излучением
Б диффузией
В броуновским движением
Г конвекцией
5. Удельная теплоемкость меди показывает
А какое количество теплоты необходимо для нагревания произвольной массы меди на один градус
Б какое количество теплоты необходимо для нагревания 1 кг меди на один градус
В какое количество теплоты необходимо для нагревания произвольной массы меди на 10 градусов
Г какое количество теплоты необходимо для нагревания 1 м3 меди на 10 градусов
6. В формулу для расчета количества теплоты, необходимого для нагревания тела входят
А объем тела, температура тела, удельная теплоемкость вещества тела
Б масса тела, температура тела, удельная теплоемкость вещества тела
В масса тела, разность температур тела после и до нагревания, удельная теплоемкость вещества тела
Г масса тела, температура тела, объем тела
7. Испарение – это
А процесс парообразования с поверхности жидкости
Б процесс парообразования со всего объема жидкости
В процесс приводящий к нагреванию жидкости
Итоговый тест по физике за 7 класс
В заданиях считать, что g=10 Н/кг
1. Физическое явление – это
А. Сила. Б. Медь. В. Килограмм. Г. Испарение.
2. Какая из перечисленных величин является единицей плотности?
А. секунда Б. Ньютон В. Паскаль Г. кг/м3
3. Какой буквой обозначают силу?
А. Р Б. S В. F Г. A
4.Галилей для изучения законов свободного падения тел изучал движение тел с наклонной плоскости. Как называются такие действия ученых?
А. Факты. Б. Гипотезы. В. Теории. Г. Опыты.
5. Мельчайшая частица вещества называется…
А. атом. Б. молекула. В. ион. Г. электрон.
6. В каком из трех состояний вещества при одной и той же температуре диффузия происходит быстрее?
А. В твердом. Б. В жидком.
В. В газообразном. Г. Во всех трех состояниях одинаково.
7. В каком состоянии вещества скорость беспорядочного движения его молекул уменьшается с понижением температуры?
А. Только в газообразном. Б. Во всех состояниях.
В. В жидком. Г. Ни в одном состоянии.
8. Тело сохраняет свой объем и форму. В каком агрегатном состоянии находится вещество, из которого состоит тело?
А. В жидком. Б. В твердом. В. В газообразном.
9. Тело объемом 20 см3 состоит из вещества плотностью 2,5 г/см3. Какова масса тела?
А. 0,125 г Б. 8 г В. 50 г Г. 50 кг
10. С какой силой притягивается к Земле тело массой 3 кг?
А. 3 Н. Б. 3 кг. В. 30 Н. Г. 30 кг.
11. Какое давление на пол оказывает ковер весом 150 Н площадью 6 м2?
А. 25 Па. Б. 90 Па. В. 900 Па. Г. 4 Па.
12. Три тела одинакового объема полностью погружены в три различные жидкости. Первая жидкость — масло, вторая — вода, третья — ртуть. В какой жидкости на тела действует меньшая архимедова сила?
А. В масле. Б. В воде. B. В ртути. Г. Во всех трех жидкостях одинаковая
13. Три тела одинакового объема полностью погружены в одну и ту же жидкость. Первое тело — стальное, второе тело — алюминиевое, третье тело — деревянное. На какое из них действует меньшая архимедова сила?
А. На стальное. Б. На алюминиевое.
В. На деревянное. Г. На все три тела действует одинаковая архимедова сила.
14. Под действием силы 10 Н тело перемещается на 4 м по направлению действия силы. Какую работу совершила сила?
А. 80 Дж. Б. 40 Дж. В. 10 Дж. Г. 5 Дж.
15. Подъемный кран поднимает вертикально вверх груз весом 1000 Н на высоту 5 м за 10 с. Какую механическую мощность развивает подъемный кран во время этого подъема?
А. 50000 Вт. Б. 10000 Вт. В. 2000 Вт. Г. 500 Вт.
16. Каким физическим прибором измеряется силу?
А. Термометром. Б. Манометром. В. Барометром. Г. Динамометром.
17. Какой энергией обладают скатывающиеся с горки санки?
А. Потенциальной. Б. Кинетической.
В. Кинетической и потенциальной.
Г. Ни потенциальной, ни кинетической.
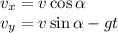

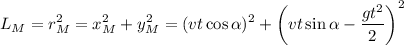
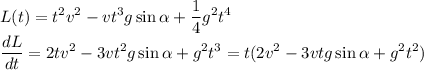
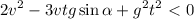
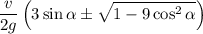
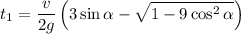
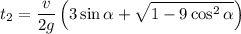
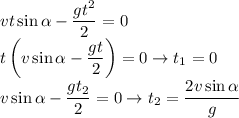
![\displaystyle t \in \left[t_1;\min\left(t_2,\frac{2v\sin\alpha}{g}\right)\right], \\ t_1=\frac{v}{2g}\left(3\sin\alpha-\sqrt{1-9\cos^2 \alpha}\right) \\ \\ t_2=\frac{v}{2g}\left(3\sin\alpha+\sqrt{1-9\cos^2 \alpha}\right) \\ \\ \alpha \in [70.53^\circ;90^\circ]](/tpl/images/0582/4256/b9998.png)
![\displaystyle \min\left(t_2,\frac{2v\sin\alpha}{g}\right)\right]-t_1](/tpl/images/0582/4256/9ff96.png)
![\displaystyle \frac{v}{2g}\left(3\sin\alpha+\sqrt{1-9\cos^2 \alpha}\right)- \frac{v}{2g}\left(3\sin\alpha-\sqrt{1-9\cos^2 \alpha}\right)= \\ \\ \frac{v}{g}\cdot\sqrt{1-9\cos^2 \alpha}, \ \alpha \in [70.53^\circ;90^\circ]](/tpl/images/0582/4256/de712.png)
теперь нужно воспользоваться теоремой остроградского-гаусса
поток вектора напряженности электрического поля через замкнутую сферическую поверхность равен заряду ограниченному єтой поверхности делить на Еo
заряд известен, он равен заряду шара, полностью находящегося внутри сферы. Ео - электрическая постоянная
Ф=q/Eo=17,7*10^(-9)/8,85 × 10^-12=2000 В*м