Question

Спортсмен массой 50кг прыгает с высоты 10м в воду. Чему равны его потенциальная и кинетическая энергия на высоте 4м относительно поверхности воды С формулой

Answer 1

2000 Дж 2997.5625 Дж

Объяснение:

Потенциальная энергия спортсмена будет равна:

$E_{n} = mgh$

где m - масса спортсмена, кг

g - ускорение свободного падения, 10 м / с²

h - высота, на которой находится спортсмен относительно воды, м

Кинетическая энергия спортсмена будет равна:

$E_{k} = \frac{mv^2}{2}$

где m - масса спортсмена, кг

v - скорость спортсмена в момент, когда он находится на высое 4 м, м

Потенциальная энергия равна:

$E_{n} = 50 * 10 * 4 = 2000$

Нам неизвестна скорость в момент, когда спортсмен находился относительно воды на высоте 4 м. Надём сначала высоту, которую он пролетел в момент падения:

$h_{2} = h_{0} - h_{1} = 10 - 4 = 6$

Надём время, которое спортсмен находится в воздухе, пока летел до отметки высоты в 4 м:

$h_{2} = \frac{gt^{2}}{2}$

$t = \sqrt{\frac{2h_{2}}{g} } = \sqrt{\frac{2 * 6}{10} } = 1.095$

Из формулы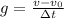 $g = \frac{v-v_{0}}{зt}$ найдём конечную скорость:

$v = gзt = 10 * 1.095 = 10.95$

Находим кинетическую энергию спортсмена:

$E_{k} = \frac{50 * (10.95)^{2}}{2} = 2997.5625$