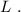 Пусть передъ тѣмъ, какъ передняя точка локомотива равняется съ наблюдателемъ – поѣздъ неограниченное время ужѣ ѣдетъ съ тѣмъ же ускореніемъ. За начало отсчета времени примемъ тотъ моментъ, когда скорость поѣзда была равна нулю. Въ такомъ случаѣ уравненіе движенія поѣзда упростится и не будетъ содержать начальной скорости, однако, когда передняя точка локомотива поравняется съ наблюдателемъ – поѣздъ ужѣ проѣдетъ нѣкоторое разстояніе
Пусть передъ тѣмъ, какъ передняя точка локомотива равняется съ наблюдателемъ – поѣздъ неограниченное время ужѣ ѣдетъ съ тѣмъ же ускореніемъ. За начало отсчета времени примемъ тотъ моментъ, когда скорость поѣзда была равна нулю. Въ такомъ случаѣ уравненіе движенія поѣзда упростится и не будетъ содержать начальной скорости, однако, когда передняя точка локомотива поравняется съ наблюдателемъ – поѣздъ ужѣ проѣдетъ нѣкоторое разстояніе 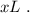
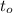 въ это мгновеніе можно выразить, какъ:
въ это мгновеніе можно выразить, какъ: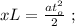
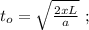 [1]
[1]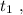 когда проѣдетъ локомотивъ:
когда проѣдетъ локомотивъ: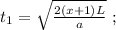
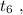 когда проѣдетъ почти вѣсь поѣздъ, но всё жъ пока-таки безъ шести вагоновъ:
когда проѣдетъ почти вѣсь поѣздъ, но всё жъ пока-таки безъ шести вагоновъ: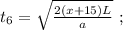
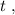 когда въ концѣ концовъ проѣдетъ вѣсь поѣздъ:
когда въ концѣ концовъ проѣдетъ вѣсь поѣздъ: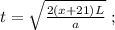 [2]
[2]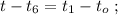
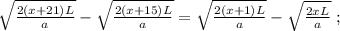
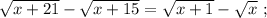
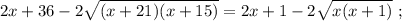
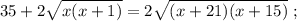
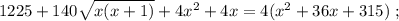
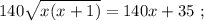
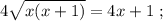
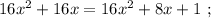
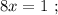
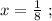
 ужѣ и слѣдуетъ отвѣтъ на вопросъ задачи:
ужѣ и слѣдуетъ отвѣтъ на вопросъ задачи: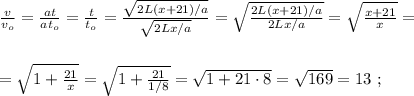
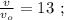
Обозначим скорость поезда в начальный момент, как
скорость, когда только один вагон проехал мимо наблюдателя:
когда только 6 последних вагонов не проехали наблюдателя:
и скорость , когда весь состав проехал мимо наблюдателя:
В соответствии с условием: интервалы времени от состояния
С другой стороны, от состояния
Сложим с [1] :
Поскольку разность квадратов краевых скоростей при одном и том же ускорении пропорциональна пройденному пути, то:
так как вся длина поезда составляет
Подставляем [2] и получаем:
Из [2]:
ОТВЕТ:
ВТОРОЙ
Запишем уравнение движения передней точки поезда относительно наблюдателя:
Обозначим длину вагона, как
Локомотив, потом почти весь состав без 6 вагонов, и затем весь состав –
– проедут через время
Вычтем из последнего – предпоследнее:
Поскольку
Учитывая [2] :
Используя [1] :
Скорость в конце прохождения всего состава, учитывая [3] :
ОТВЕТ: