1)Дифракционная решетка, постоянная которой равна 0,004 мм, освещается светом с длиной волны 687 нм. Под каким углом к решетке нужно проводить наблюдение, чтобы видеть изображение спектра второго порядка.
2)На дифракционную решетку, имеющую 500 штрихов на 1 мм, падает монохроматический свет длиной волны 500 нм. Свет падает на решетку перпендикулярно. Какой наибольший порядок спектра можно наблюдать?
3)Дифракционная решетка расположена параллельно экрану на расстоянии 0,7 м от него. Определите количество штрихов на 1 мм для этой дифракционной решетки, если при нормальном падении на нее светового пучка с длиной волны 430 нм первый дифракционный максимум на экране находится на расстоянии 3 см от центральной светлой полосы. Считать, что sinφ ≈ tgφ.
Формула дифракционной решетки
для малых углов
тангенс угла = р-ние от ц максимума / р-ние до экрана
период решетки
число штрихов единицу длины ( на мм)
4)Дифракционная решетка, период которой равен 0,005 мм, расположена параллельно экрану на расстоянии 1,6 м от него и освещается пучком света длиной волны 0,6 мкм, падающим по нормали к решетке. Определите расстояние между центром дифракционной картины и вторым максимумом. Считать, что sinφ ≈ tgφ.
5)Дифракционная решетка с периодом 10-5 м расположена параллельно экрану на расстоянии 1,8 м от него. Решетка освещается нормально падающим пучком света длиной волны 580 нм. На экране на расстоянии 20.88 см от центра дифракционной картины наблюдается максимум освещенности. Определите порядок этого максимума. Считать, чтоsinφ ≈ tgφ.
Объяснение:
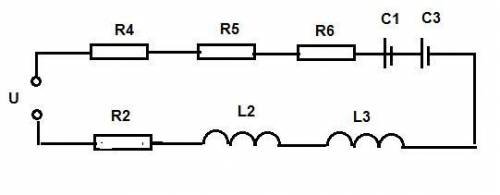
Дано:
U=270 B
R2 = 12 Ом
R4 = 22 Ом
R5 = 16 Ом
R6 = 10 Ом
L2 = 14 мГн
L3 = 8 мГн
C1 = 11 мкФ
C3 = 22 мкФ
ν = 50 Гц
_________
1)
Находим активное сопротивление цепи:
R = R2+R4+R5+R6 = 12+22+16+10 = 60 Ом
2)
Находим реактивные сопротивления катушек:
XL = XL2+XL3 = 2π*ν*L2+2π*ν+L3 = 2π*ν*(L2+L3)=
=2*3,14*50*(14+8)*10⁻³ ≈ 69 Ом
3)
Находим реактивное сопротивление емкостей:
Xc = Xc1+Xc3 = 1 / (2π*ν*C1) + 1/(2π*ν*C3) = 1/(2π*ν)*(1/C1+1/C3) =
= 1/(2*3,14*50) * (1/11*10⁻⁶+1/22*10⁻6) ≈ 1/(2*3,14*50)*(1/11e-6+1/22e-6)≈434 Ом
4)
Находим общее сопротивление цепи:
Z = √ (R²+ (Xc-XL)²) = √ (60² + (434-69)²) ≈ 670 Ом
5)
Находим общий ток:
I = U / Z = 270 / 670 ≈ 0,4 А
6)
Находим активную мощность:
P =I²*R = 0,4²*60 = 9,6 Вт
7)
Ну а теперь последовательно находим напряжения на элементах цепи:
Резисторы:
U2 = I*R2 = 0,4*12 = 4,8 B
U4 = I*R4 = 0,4*22 = 8,8 B
U5 = I*R5 = 0,4*16 = 6,4 B
U6 = I*R6 = 0,4*10 = 4,0 B
На катушках:
UXL2 = 2*π*ν*L2*I = 2*3,14*50*14*10⁻³ *0,4 ≈ 1,8 B
Аналогично на XL3 (рассчитать самостоятельно!)
Напряжение на конденсаторах:
UXc1 = I*(1/(2π*ν*C) = 0,4*1/(2*3,14*50*11*10⁻⁶) ≈ 116 В
(Аналогично на другом конденсаторе рассчитать самостоятельно)
Электрическая схема:
Общее сопротивление цепи при последовательном соединении проводников:
R = R₁ + R₂ + ... + Rₓ
Тогда для двух последовательно соединенных ламп:
R = 150 + 200 = 350 (Ом)
Сила тока в цепи при последовательном соединении проводников:
I = I₁ = I₂ = ... = Iₓ
Тогда:
I = I₁ = I₂ = U/R = 100 : 350 ≈ 0,29 (A)