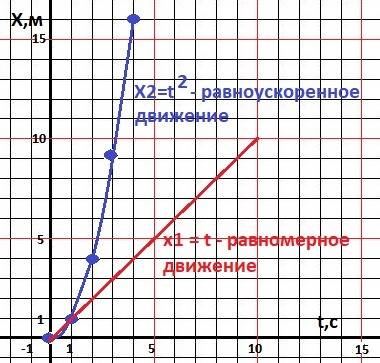
Рисунок к задаче в приложении.
Равномерное движение описывается формулой
X(t) = Xo + V*t, где: Хо - начальное смещение, V - скорость движения.
График равномерного движения - квадратичная парабола. На рисунке - Xo = 0, V = 1,
При равномерном движении промежутки за равные интервалы времени будут одинаковыми - как и скорость, а их разность равна нулю - ускорение =0 - равномерное движение.
По графику функции можно сразу определить и Хо - сдвиг по оси Х и V - (коэффициент наклона прямой).
Равноускоренное движение описывается формулой
X(t) = Xo + Vo*t + a*t²/2, а графиком будет парабола. На рисунке: Хо=0, Vo=0, a = 2.
В этом случае разности перемещений за одинаковое времени будут составлять арифметическую прогрессию с разностью - d = 2 - ускорение движения.
Например, из рисунка находим значения перемещений:
Х = 1, 4, 9, 16, 25 - перемещения.
Находим первую разность и получим:
V = 3, 5, 7, 9 - скорости - равномерно увеличиваются.
Находим вторую разность и получим:
a = 2, 2, 2 - ускорение - постоянное - равноускоренное движение.
По формуле давления твёрдых тел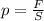
, где F - сила давления (Н), S - площадь опоры (м²). Действующее давление определяем по формуле давления жидкостей 
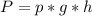, где р - плотность вещества (кг/м³), g - ускорение свободного падения (g = 9,8 м/с² ≈ 10 м/с²). h - высота столба жидкости (м). Сила действует со стороны
произвонимое давление будет равна половине давленияна дно пробки т.е.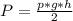
. Подставляем в формулу давления твёрдых тел: 
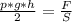, из данного выражения выражаем находимую высоту: 
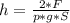. В системе СИ: 15 см² = 15*10⁻⁴ м²; плотность воды р = 1000 кг/м³. Подставляем численные данные и вычисляем: 