Объяснение:
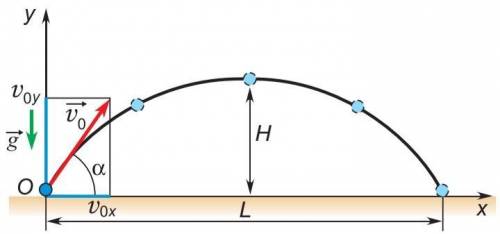
1) форму параболы ( с вершиной параболы в высшей точке траектории )
2) В начале движения тела с начальной скоростью ( v0 ) проекция которой на ось Ох ( v0x ) равна ( v0cosα ) , a на ось Оу ( v0y ) равна ( v0sinα )
В высшей точки траектории vy = 0 м/с
Поэтому
0 = v0sinα - gt
отсюда
tп. ( время подъема ) = t = ( v0sinα ) / g
Дальность полёта тела будет вычисляться как
L = vxtпол.
Где tпол. ( полное время движения ) = 2tп. = ( 2v0sinα ) / g
L = ( v0cosα2v0sinα ) / g
2sinαcosα = sin2α , поэтому
L = ( v0²sin2α ) / g
Но sin90° = 1 , поэтому если α = 45° , то sin2α = 1
Поэтому именно при угле бросания равным 45° будет максимальная дальность полета
3) В наивысшей точке траектории скорость тела сонаправлена с осью горизонта , поэтому угол между горизонтом и вектором скорости тела в данный момент времени равен 0°
Так как траекторией движения тела брошенного под углом является парабола тогда в конечной точке траектории угол между горизонтом и вектором направления направления скорости будет равен углу между вектором начальным скорости и горизонтом .
Силу трения можно не учитывать, она одинакова для первого и второго вагонов. Пусть между локомотивом и первым вагоном сила натяжения равна Т₁, между первым и вторым вагонами Т₂.
Тогда II з-н Ньютона в проекции на ось ОХ, направление которой совпадает с направлением движения запишется для первого вагона так: Ма = Т₁ - Т₂
А для второго так: Ма = Т₂
Решая эту простенькую систему получим, что Т₁ = 2Ма; Т₂ = Ма.
Отсюда Т₁/Т₂ = 2.