Объяснение:
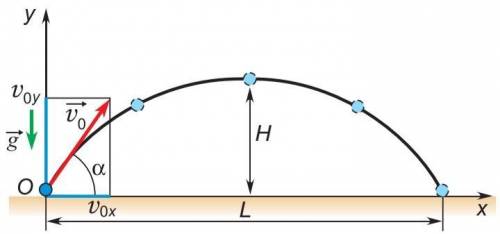
1) форму параболы ( с вершиной параболы в высшей точке траектории )
2) В начале движения тела с начальной скоростью ( v0 ) проекция которой на ось Ох ( v0x ) равна ( v0cosα ) , a на ось Оу ( v0y ) равна ( v0sinα )
В высшей точки траектории vy = 0 м/с
Поэтому
0 = v0sinα - gt
отсюда
tп. ( время подъема ) = t = ( v0sinα ) / g
Дальность полёта тела будет вычисляться как
L = vxtпол.
Где tпол. ( полное время движения ) = 2tп. = ( 2v0sinα ) / g
L = ( v0cosα2v0sinα ) / g
2sinαcosα = sin2α , поэтому
L = ( v0²sin2α ) / g
Но sin90° = 1 , поэтому если α = 45° , то sin2α = 1
Поэтому именно при угле бросания равным 45° будет максимальная дальность полета
3) В наивысшей точке траектории скорость тела сонаправлена с осью горизонта , поэтому угол между горизонтом и вектором скорости тела в данный момент времени равен 0°
Так как траекторией движения тела брошенного под углом является парабола тогда в конечной точке траектории угол между горизонтом и вектором направления направления скорости будет равен углу между вектором начальным скорости и горизонтом .
Лодка продвинулась носом (в сторону. противоположную движению человека) на 0,5 м.
Объяснение:
ДАНО
m = 60 кг - масса человека
М = 180кг - масса лодки
s = 2 м - перемещение человека относительно лодки
НАЙТИ
х - ? - перемещение лодки
РЕШЕНИЕ
При переходе человека ближе к корме центр тяжести системы "человек-лодка" не должно измениться.
Пусть до осуществления перехода центр масс лодки и человека совпадали (человек, скажем, стоял в центре лодки). Координата центра масс системы была равна нулю
Когда человек сместился к корме на 2 м, лодка переместилась в противоположном направлении на х м, и центр масс системы остался на прежнем месте. Тогда получается, что человек относительно общего центра масс сместился к корме на (2 - х) м.
Составим уравнение для координаты центра масс
0 = - М · х + m · (2 - x)
(М + m) · x = 2m
x = 2m : (M + m)
x = 2 · 60 : (180 + 60) = 0.5 (м)