Разность весов тел в воздухе (20 Н) и в воде (17 Н), будет выталкивающей силой т.е. силой Архимеда. Тогда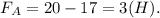 
. Полкчили что Архимедов сила равна 3 Н.
По формуле закона Архимедовой силы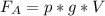 
, где р - плотность вещества (кг/м³), V - объём (м³), g - ускорение свободного падения (g = 9,8 м/с² ≈ 10м/с²).
Отсюда выразим объём тела: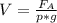 
. За плотность принимем плотность жидкости в которой находится тело, в данном случае воды: р = 1000 кг/м³. Подставляем и вычисляем: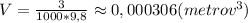 
Объём тела, есть отношение массы тела к велечине его плотности т.е. 
. Вес тела в воздухе весит 20 Н при этом его масса воздухе состовляет 2 кг.
Тогда Из формулы объёма тела выражаем находимую плотность: 
Подставленм и вычисляем: 
l = 400 м
Первый бегун пробежал тогда: lk + lλ = v₁t, где 0 ≤ λ ≤ 1, k∈|Ν.
Второй соответственно пробежит lm+lλ = v₂t. m∈|Ν.
Какой смысл этих уравнений: в момент встречи оба бегуна должны встретится в одной точке, которая характеризуется расстоянием до старта
0 ≤ r < l. r ≡ lλ. При этом каждый из них может пробежать разное число целых кругов.
Теперь составим разность этих уравнений и обозначим s = m-k
Тогда, ls = (v₂ - v₁)t, преобразуя получим:
Из данного выражения умножая на скорость каждого бегуна можно получить соответствующее расстояние.
Теперь случай, когда они бегут в разные стороны.
Точка встречи по прежнему характеризуется расcтоянием r = λl, причём оно будет измеряться по ходу движения первого бегуна.
Т.е. уравнение для первого будет:
lk + lλ = v₁t
А для второго:
lm + l(1-λ) = v₂t
Сложим их и получим:
где d = m+k+1 - любое натуральное число.
Видно, что при d = 1 мы получили обычною формулу для встречного движения.
P.S. Данное решение проведено не совсем формально. Было бы правильнее задать криволинейную ось по стадиону и учитывать знаки скоростей в проекцию на неё, а вместо пути писать координату на ней, но для большей наглядности мы рассматривали модули величин, сразу учитывая, какая скорость больше.