дано
vx=540 км/ч=150 м/с
g=10 м/с2 (возможно 9.8 м/с2)
h=2 км=2*10^3 м
---------------------------
v -?
решение
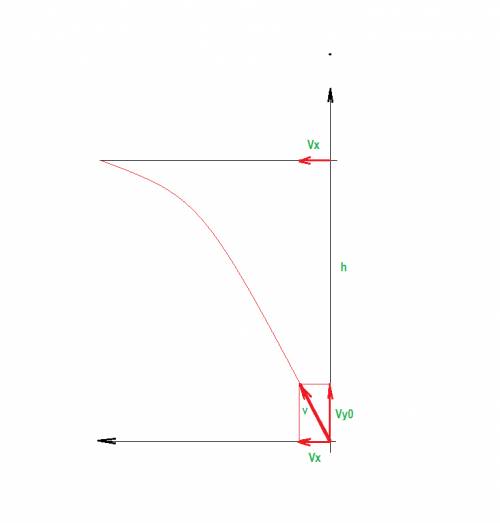
Рисунок прилагается.
По условию самолет находится точно над орудием. Чтобы не отстать от самолета или не обогнать его снаряд должен иметь скорость самолета по оси Х. vx=150 м/с
По условию скорость снаряда имеет наименьшее значение. Значит конечная скорость по оси Y vy=0. Начальную скорость vy0 найдем из формулы h = (vy^2 –vy0^2) /(-2g) ; при равнозамедленном движении ускорение имеет отрицательное значение vy0 =√(2gh)
Начальная скорость снаряда по теореме Пифагора
v = √ (vx^2+vy0^2)= √ (vx^2+2gh)= √(150^2+2*10*2*10^3)=250 м/с
ответ 250 м/с
1) Х(01)=2м
2) Х(02)=0м
V(1)=4+6t
V(2)=5+20t
a(1)=6м/с^2
а(2)=20м/с^2
t(встречи)=0,5с
Х(встречи)=4,75м~5м
Объяснение:
Дано:
Х(1)=2+4t+3t^2
X(2)=5t+10t^2
X(01)=?
X(02)=?
V(1)=?
V(2)=?
a(1)=?
a(2)=?
При t=0 Х(01)=2+4×0+3×0=2(м)
При t=0 X(02)=5×0+10×0=0(м)
V(1)=X(1)'=2'+(4t)'+(3t^2)'=
=4+3×2t=4+6t
V(2)=X(2)'=(5t)'+(10t^2)'=5+20t
a(1)=(V(1))'=(4+6t)'=6(м/с^2)
а(2)=(V(2))'=(5+20t)'=20(м/с^2)
Определим время встречи
2+4t+3t^2=5t+20t^2
7t^2+t-2=0
D=1-4(-14)=57>0
t(1)=-1+57^1/2/ 14=0,5c
t(2)=-1-57^1/2/ 14<0 этот вариант
не рассматриваем, так как встре
ча произошла до начала наблю
дения.
Определим место встречи
х(1)=2+4×0,5+3×0,5^2=
=2+2×0,75=4,75~5м