Question

решить, если то я сессию сдам! Я буду очень благодарен. Желательно с решениями!

Answer 1

4.2.2 Так как не указана масса чайника, решу просто для воды

Количество теплоты, затраченное на нагревание воды

$Q=cm\Delta t=4200*0.45*90=170100$ Дж

Время закипания

$t=\frac{Q}{P}=\frac{170100}{500}=340$ c

4.2.3 Составим уравнение теплового баланса, обозначив за х установившуюся температуру

$m_{ice}\lambda+c(m_B+m_{ice})x=m_pL+cm_p(100-x)$

Подставим данные из условия

$0.06*3.4*10^5+4200*0.56*x=0.01*2.3*10^6+4200*0.01*(100-x)$

$20400+2352x=23000+4200-42x$

$2394x=6800$

$x=2.8$ °C

4.2.4 Самая интересная задача.

Объем тела при нагревании увеличивается, эта зависимость выражается формулой

$V=V_0(1+\beta t)$ где β - коэффициент объемного теплового расширения, для чугуна $3.3*10^-^5$ 1/К

Плотность также зависит от температуры

$\rho=\frac{m}{V}=\frac{m}{V_0(1+\beta t)}=\frac{\rho_0}{(1+\beta t)}$

Выразим отсюда температуру

$t=\frac{\rho_0}{\rho \beta} -\frac{1}{\beta }$

Плотность чугуна до того, как он остыл

$\rho =\frac{m}{V}=\frac{0.325}{48*10^-^6}=6771$ кг/м³

Значит чугун был взят при температуре

$t=\frac{6800}{6771*3.3*10^-^5}-\frac{1}{3.3*10^-^5} =130$ °C

Дальше все просто

Чугун остывая до нуля градусов Цельсия отдаст количество теплоты

$Q=cm\Delta t=500*0.325*130=21125$ Дж

Масса растаявшего льда

$m=\frac{Q}{\lambda}=\frac{21125}{0.33*10^6}=0.064$ кг или 64 г

4.2.5 Просто найдем массу воды

$m=\frac{Q}{L}=\frac{756000}{2.3*10^6}=0.329$ кг или 329 г

4.2.6 Кинетическая энергия конькобежца

$E_k=\frac{mv^2}{2}=\frac{55*8.5^2}{2}=1987$ Дж

На таяние льда пойдет половина этой энергии то есть 994 Дж, масса растаявшего льда

$m=\frac{994}{330000}=0.003$ кг или 3 г

4.2.7 Изменение кинетической энергии пули

$\Delta E_k=\frac{m}{2}(v_2^2-v_1^2)=\frac{0.025}{2}*(400^2-250^2)=1219$ Дж

Пуля поглотит половину, т.е. 610 Дж

а)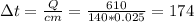 $\Delta t=\frac{Q}{cm}=\frac{610}{140*0.025} =174$ °С

б) Ее температура будет 174+20=194 °С - это ниже температуры плавления свинца (327 °С), значит пуля не расплавится.