Речь скорее всего идет о Лабораторной работе , с которой сталкиваются все студенты первого курса любого института, приступая к изучению курса физики.
Лабораторная работа посвящена измерению ускорения свободного падения с машины Атвуда.
Классический опыт с измерением времени падения тела осуществить сложно, так как требуется очень большая точность измерения времени плюс сопротивление воздуха играет значительную роль. Приходится увеличивать высоту и время измерения. Галлилей для своих опытов использовал Пизанскую башню.
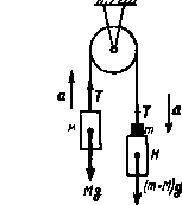
Поэтому была придумана машина Атвуда. Схема ее на рисунке.
Через блок перекинута нить, на которой закреплены грузы массой М каждый. На один грузов кладется перегрузок массой m.
Уравнения движения
Mg - T = -Ma
(М + m) g - Т = (М +m) а
Из уравнений
a = gm / ( 2M+m)
а время с высоты h равно
t = √(2h/a)
Это время уже достаточно большое и может быть измерено с меньшей точностью, для получения требуемой точности измерения величины g.
Большое значение в этой работе как раз уделено не самому процессу измерения g ( которое конечно всем известно ) , а оценке среднего его значения и точности ее измерения, абсолютной и относительной ее погрешности. Вот на этом то все студенты первого курса и "плавают" ))
ответ: 9,81 м/с²
Объяснение:
Для определения среднего значения ускорения свободного падения нам потребуется сверхточный секундомер ( допустим он у нас есть ) ну и хорошая измерительная лента ( допустим рулетка )
Поднимем тело относительно Земли на высоту 1,5 м а затем его отпустим ( без начальной скорости ) наш сверхточный секундомер показывает то что тело падало в течении 0,553 с повторим наш опыт 5 раз и найдём среднее значение промежутка времени в течение которого падало тело спустя некоторое время с секундомера мы определили что этот промежуток составил 0,553 с
Так как в нашем эксперименте мы тело отпускали без начальной скорости тогда
h = ( gt² )/2
Отсюда
g = ( 2h )/t² ≈ 9,81 м/с²
То есть значение ускорения свободного падения которые мы получили составляет 9,81 м/с² что отлично согласуется с реальными численными данными
Формула электрического сопротивления:
По условию мы изменяем l, и длину проводника мы увеличили на 0,2%.
Для того, чтобы математически записать это удлинение, надо 0,2% представить в долях, а для того чтобы проценты перевести в доли надо проценты делить на 100.
0,2%=0,2/100=0,002
Следовательно длина вместо l, стала (l+0,002*l), то есть стала 1,002*l.
По условию плотность проводника не изменилась после удлинения, обозначим её тоже как удельное электрическое сопротивление, то есть как ρ, но будем понимать что это разные вещи.
Объём до удлинения:
V=m/ρ
Так как m=const, то есть величина постоянна и она не измена, так как масса не может изменяться, тогда объём после удлинения:
V=m/ρ
Итог: объём после удлинения не изменился.
Но объём можно записать по-другому, так как проводник у нас цилиндрической формы, то для него справедлива математическая формула объёма цилиндра, то есть надо умножить его длину, на площадь основания (как раз таки площадь поперечного сечения S), тогда:
До удлинения:
V=l*S
После удлинения:
V=l2*S2=1,002*l*S2
Выразим S с формулы до удлинения и после удлинения, получим:
До удлинения:
S=V/l
После удлинения:
Мы узнали на сколько изменилась площадь поперечного сечения, значит теперь посмотрим на сколько процентов увеличилось электрическое сопротивление:
Следовательно R2 больше R1 в 1,004.
Переведём доли в проценты, для этого доли умножим на сто.
1,004*100=100,4%
То есть R2 больше R1 на:
100,4%-100%=0,4%
ответ: электрическое сопротивление проводника стало больше на 0,4%.Объяснение: