1. T=3,14 мс; Ню=318 Гц
2. C=1,25 мкФ
3. изменилась в 0,2 раза
4. изменилась в 2 раза
Объяснение:
давай начну с обозначения:
период - T, частота - Ню, циклической частоты (или центростремительная) - w, ёмкость конденсатора - С, катушку индуктивности - L, П=3,14
1. период равен: T=2П√(C*L)
тогда T=2*3,14*0,5*10^-3=3,14 мс
частота равна: Ню=1/T
Ню=1/(3,14*10^-3)=318 Гц
2. период равен: T=2П√(C*L)
отсюда выводим: C=T^2/(40*L)=1,25*10^-6 Ф
3. циклическая частота равна: w=2П*Ню=2П/T
период равен: T=2П√(C*L)
тогда: w=2П/2П√(C*L)=1/С(C*L)
5w0=w, так как уменьшили, то циклическая частота в начале опыта была больше на √25, т.е. на 5, следовательно конечная циклическая частота изменилась в 1/5=0,2 раза
4. период равен: T=2П√(C*L), а нам известно, что емкость конденсатора увеличилось в 4 раза, то конечный период больше начального в √4 раза, т.е. в 2 раза
Будем считать, что все элементы соединены последовательно.
Индуктивное сопротивление катушки
где f – частота, Гц.
Емкостное сопротивление конденсатора
Эквивалентное полное сопротивление цепи
Для нахождения мощности следует оперировать действующим значением напряжения. Зная амплитудное значение, найдем действующее (при этом будем исходить из того, что сигнал синусоидальный):
Тогда полная мощность в цепи
Следует учесть, что выделяется в цепи только активная мощность (на активном сопротивлении R), тогда как реактивная попеременно запасается и отдается обратно в сеть.
Активную мощность определим с коэффициента мощности, численно равного отношению активного сопротивления к полному:
cos φ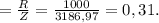
Выделяемая в цепи активная мощность
P = S*cos φ = 1,57*0,31 = 0,5 Вт.