Из условия видно, что период увеличивается, следовательно лифт должен двигаться с ускорением, направленным вертикально вниз. (Данный факт следует из формул о весе тела, его движении вверх, или вниз с ускорением, так же, можно получить из второго закона Ньютона, расписывая силы, действущие на груз, который подвешен на математическом маятнике). ( длина маятника (l) - величина постоянная).
Запишем формулу периода математического маятника:
Теперь запишем данную формулу для двух случаев:
Возведем в квадрат и правую и левую часть каждого уравнения:
V1 = 5*10 л 1л = 1дм.м3. V1 = 50 л = 0,05 м3 ; t1 = 10 град.по С V2 = 60 л = 0,06 м3 ; V2 = 6* 10 л надем массу воды: t2 = 90 град по С м1 = D*V1=1000*0,05=50 кг; м2 = 60 кг; t3 - ? Q1 = cm1(t3-t1); Q2 = cm2(t2-t3); Q1 =Q2, значит: cm1(t3-t1) = cm2(t2-t3); c- сокращается. затем раскрываем скобки группируем члены, содерж-е (t3) в одной части уравнения и находим t3 = m1t1+m2t2/m1+m2, подставляем сюда числа и получаем ответ: t3 = 54 град поС
Дано:
T1= 1 секунда.
T2=1,1 cекунда.
a=?
_______
Из условия видно, что период увеличивается, следовательно лифт должен двигаться с ускорением, направленным вертикально вниз. (Данный факт следует из формул о весе тела, его движении вверх, или вниз с ускорением, так же, можно получить из второго закона Ньютона, расписывая силы, действущие на груз, который подвешен на математическом маятнике). ( длина маятника (l) - величина постоянная).
Запишем формулу периода математического маятника:
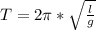
Теперь запишем данную формулу для двух случаев:
Возведем в квадрат и правую и левую часть каждого уравнения:
Поделим первое уравнение на второе:
Теперь выведем ускорение (а):
Посчитаем сначала периоды:
a=(g*(T2^2-T1^2)/(T1^2)=(g*(1,21-1)/(1,21)=0,17*g;
Подставляем значение ускорения свободного падения, равное, если быть более точным, 9,8 м/с^2.
a=0,17*9,8=1,666 м/с^2. Такое ускорение у лифтра. (если брать g=10м/с^2, то получим а=1,7 м/c^2).
ответ: а=1,666 м/с^2; (a=1,7 м/с^2).Лифт движется с ускорением, направленным вертикально вниз.