"ПЛАВНЫЙ ПОВОРОТ"
Можно сказать, что это не сказка, а воспоминание о жизни наших первобытных Землян.
Началось с того, что они двигались прямолинейно. Быстро или медленно, вперёд или назад. В результате всегда возвращались в свою пещеру. Тормозить они всё-таки могли и, поэтому лоб свой не разбивали.
Оказалось, что нужно поворачивать на поперечную дорогу.
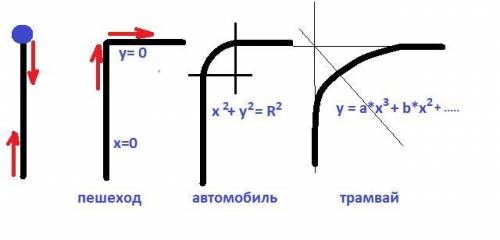
Если перекресток перпендикулярная улица - скорость резко меняет направление. (рисунок в приложении) . Такое могут сделать пешеходы на малой скорости.
Но приехали автомобилисты - им медленно ехать не хочется. И стали делать повороты на улицах с большим (и не очень большим) радиусом.
Это уравнение окружности - второго порядка.Скорость остается постоянной, а ускорение меняет направление.
Автомобилистам легко - какой хочешь радиус выбирай, а вот трамвай по рельсам едет. Он не может даже чуть-чуть изменить трассу и вот тут стали укладывать повороты по уравнению третьей степени. Теперь и ускорение плавно изменяется и скорость плавно изменяется и направление плавно изменяется.
А кто придумывал такие разные решения для строительства дорог - УЧЁНЫЕ. Главное в этом хорошие знания и математики и физики.
Это, конечно, не сказка, а быль.
Объяснение:
Дано:
L=10 мГн, C1=360 пФ, C2=40 пФ, λ−?
Решение задачи:
Частоту электромагнитных волн, которые принимает радиоприемник, можно определить по формуле:
ν=12πLC−−−√(1)
В этой формуле L – индуктивность катушки радиоприемника, C – общая электроемкость конденсаторов радиоприемника.
Известно, что электромагнитные волны распространяются со скоростью света c (в вакууме она равна 3·108 м/с). Между скоростью распространения электромагнитных волн (скоростью света c), частотой их колебаний ν и длиной волны λ существует следующее соотношение:
c=λν
λ равна:
λ=cν
В эту формулу подставим выражение (1):
λ=2πcLC−−−√(2)
Известно, что параллельно соединенные конденсатора емкостью C1 и C2 имеют общую емкость C, которую можно определить по формуле:
C=C1+C2
Подставив это выражение в формулу (2), получим:
λ=2πcL(C1+C2)−−−−−−−−−−√
Численный ответ задачи равен:
λ=2⋅3,14⋅3⋅10810⋅10–3⋅(360⋅10–12+40⋅10–12)−−−−−−−−−−−−−−−−−−−−−−−−−−√=3768м
ответ: 3768 м.
Источник: https://easyfizika.ru/zadachi/kolebaniya-i-volny/elektricheskij-kolebatelnyj-kontur-radiopriemnika-soderzhit-katushku-induktivnosti