1. am=F-Fтрения
am=F-kmg
F=am+kmg
F=m(a+kg)
m=25000/2,1
m=11 904 кг.
3. начальная скорость - v(0)=15 м/с
конечная скорость - v(k) = 0 м/с (так как он в самом верху остановится, прежде чем падать обратно)
ускорение свободного падения - g=10 м/с^2
Найти: время (t)
из формулы ускорения g=( v(k) - v(0) ) / t выводим
t = ( v(k) - v(0) ) / g
t = (0 м/с - 15 м/с) / (-g) (-g - ускорение свободного падения направлено против вектора ускорения камня)
t = -15 м/с / -10 м/с^2
t= 1,5 с
ответ: t=1,5 с.
4. m1 = 50 килограмм - масса мальчика, ловящего мяч;
m2 = 500 грамм - масса мяча;
v2 = 3 м/с (метров в секунду) - скорость мяча до взаимодействия с мальчиком.
Требуется определить v1 (м/с) - скорость мальчика после взаимодействия с мячом.
Переведем единицы измерения массы в систему СИ:
m2 = 500 грамм = 500 * 3-3 = 500 / 1000 = 0,5 килограмм.
Тогда, по закону сохранения импульса (количества движения), получаем:
m2 * v2 = (m1 + m2) * v1;
v1 = m2 * v2 / (m1 + m2);
v1 = 0,5 * 3 / (50 + 0,5) = 5 / 50,5 = 0,1 м/с (результат был округлен до одной десятой).
ответ: скорость мальчика после взаимодействия будет равна 0,1 м/с.
Объяснение:
Пусть рабочим телом является 1 моль идеального газа, находящийся в следующих состояниях для четырех характерных точек А, В, С, D цикла Карно. Учтем, что на участках АВ и ВС газ расширяется (из рисунка видно, что давление падает), то есть совершает положительную работу, а на участках CD и DA работа отрицательна. На участке ВС: A(BC)=-dU=-cv(Tx - Tr), а на участке DA: A(DA)=-cv(Tr - Тх). Для обратимого процесса dU=0 и при нахождении общей работы за цикл A(BC) и A(CD) сокращаются, и остается только разность Q(AB)-Q(CD) при изотермических процессах (при Т(АВ) и T(CD)). Поэтому А= Q(AB)-Q(CD).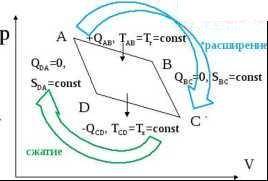
V= m/p
V1= 3,5*15=52,5л.
V2= 3,5:1,2=2,91л.
V2= 2,91*15=43,65л.
52,5-43,65=8,85 л.
Чем выше плотность тем меньше объем, в данной задачи масса шара одинакова в обоих случаях.
Ответ: Суммарный объем шаров уменьшился на 8,85 л.