ДАНО
L
H
-------------------------
S - ?
РЕШЕНИЕ
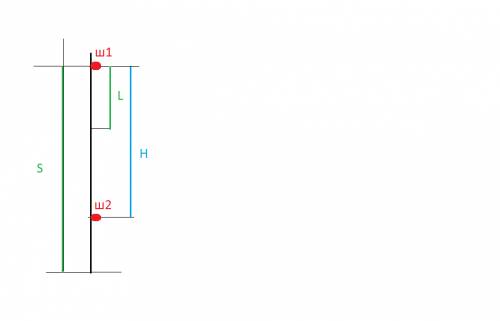
Обозначим S- высота башни
Сразу понятно, что L не равно H .(см на рисунке)
ШАРИК 1
начальная скорость V1o=0
в конце отрезка L имеет скорость V (найдем, нужда для решения)
L=(V^2-V1o^2)/2g=V^2/2g
V=√(2gL) (1)
за остальное время t - шарик 1 пролетел расстояние S-L (с начальной скоростью V)
S- L = Vt +gt^2/2 (2)
ШАРИК 2
начальная скорость V2o=0
S- H высота , с которой началось падение
падение длилось тоже время t
S-H = V2ot +gt^2/2 = gt^2/2 (3)
S-H = gt^2/2
t^2 =2(S-H)/g
t =√(2(S-H)/g ) (4)
подставим (1)(3)и(4) в (2)
S- L = Vt +gt^2/2 = √(2gL) *√(2(S-H)/g ) + (S-H)
S- L- (S-H) = √(2gL) *√(2(S-H)/g)
H-L =√(4L(S-H))
(H-L)^2 =4L(S-H)
S-H=(H-L)^2 /(4L)
S= (H-L)^2 /(4L) + H
ответ высота башни (H-L)^2 /(4L) + H
Так. Ось х направляем по ходу движения первого тела.
Уравнение для первого тела, двигающегося равноускоренно: x = 0 + 3t + 2t^2/2
Уравнение для второго тела. двигающегося равномерно: х = -5t
Первое тело успело пройти 1 секунду: х = 3*1 + 1 = 4 метра. Получается что обоим телам нужно пройти 96 метров. Но так скорость первого тела к этой секунде уже изменилась V = V0+at = 3+2*1=5м/с. Получаем новое уравнение: x = 0 + 5t + 2t^2/2
Теперь приравниваем уравнения: 5t + t^2 = -5t = 96
t^2 + 10t - 96 = 0
D=484 ; х1=-16(не подходит по условию) , х2=6секунд.
Прибавляем к этому еще одну секунду которую шло первое тело, ответ 7 секунд.
1. А) конвекция
Объяснение: