1. Пусть длина нити равна L. Отклонив шарик на нити на угол а от вертикали, его приподнимают на высоту, равную h, и тем самым сообщают потенциальную энергию, равную W пот = mgh; Если нить отпустить, то, падая с этой высоты, шарик достигает скорости v, определить которую можно, зная, что вся его потенциальная энергия превратилась в кинетическую Wпот = Wкин ; Wпот= mgh; Wкин= mv(кв)/2; v(кв) = 2gh. Находим эту высоту. Сделайте чертеж Из точки подвеса А проводим вертикальную прямую и на эту прямую опустим перпендикуляр из точки В, в которой находится шарик при отклонении на угол а. Получим прямоугольный треугольник АВС. Высота h, на которую поднят шарик, равна OD – OC; OD = OB = L; h = L – L cosa = L(1 – cosa).
v(кв) = 2g L(1 – cosa). v = «корень квадратный» из 2g L(1 – cosa). Это и есть ответ. Чем больше угол отклонения, тем меньше значение cosa , и тем больше максимальная скорость.
2. mgh=mvквадрат/2+Aсопр, где Асопр=Fh=mgh - работа сил сопротивления, тогда F=(mgh-mvквадрат/2)/h=1,4Н
Постараюсь расписать как можно подробней.
Нам нужно найти E
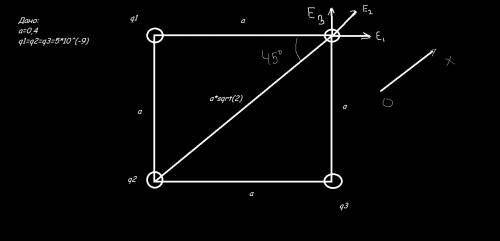
Для начала нужен рисунок(см. вложения)
Запишем уравнение в векторном виде:
E (вектор)=E1(вектор)+E2(вектор)+E3(вектор)
Теперь проецируем на ось Ох(см.рисунок)
E=E1*cos45+E2+E3*cos45;
E=k*q/a^2(формула, которой мы пользуемся)
Получим:
E=k*q/a^2*sqrt(2)/2+k*q/2a^2+ k*q/a^2*sqrt(2)/2=2k*q/a^2*sqrt(2)/2+k*q/2a^2=k*q/a^2(sqrt(2)+1/2)=9*10^(9)*5*10^(-9)/16*10^(-2)*(sqrt(2)+1/2)=281,25*1,9=538,4
ответ: E= 538,4
Вроде как, не где не ошибся.
Если что-то непонятно напишите мне об этом.
найдём силу тока I = P/U = 600/220 = 2.7А
найдём сопротивление R = U/i = 81 Ом
найдём энергию Q = I2*R*t = 7.3*81*7200 = 4257360Дж