
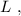 и жёсткостью
и жёсткостью 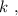 деформацию которой обозначим, как
деформацию которой обозначим, как 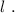 Тогда возникающая сила упругости при её деформации будет выражаться обычным законом Гука:
Тогда возникающая сила упругости при её деформации будет выражаться обычным законом Гука: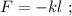
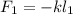
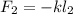

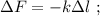
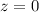 – все силы, действующие на груз, взаимно скомпенсированы. При изменении положения груза на
– все силы, действующие на груз, взаимно скомпенсированы. При изменении положения груза на 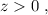 (т.е. вверх), растяжение нижней пружины (down) увеличится, а значит её сила, действующая на груз вниз – тоже увеличится по модулю. В проективном виде это изменение выразится, как:
(т.е. вверх), растяжение нижней пружины (down) увеличится, а значит её сила, действующая на груз вниз – тоже увеличится по модулю. В проективном виде это изменение выразится, как: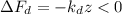 – это символизирует увеличение отрицательной (направленной вниз) величины силы нижней пружины.
– это символизирует увеличение отрицательной (направленной вниз) величины силы нижней пружины.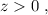 (вверх), растяжение верхней пружины (up) уменьшится, а значит её сила, действующая на груз вверх – тоже уменьшится по модулю. В проективном виде это изменение выразится, как:
(вверх), растяжение верхней пружины (up) уменьшится, а значит её сила, действующая на груз вверх – тоже уменьшится по модулю. В проективном виде это изменение выразится, как: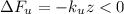 – это символизирует уменьшение положительной (направленной вверх) величины силы верхней пружины.
– это символизирует уменьшение положительной (направленной вверх) величины силы верхней пружины.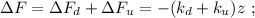
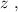 общая сила, действующая со стороны системы пружин – будет как раз и равна изменению действующих сил:
общая сила, действующая со стороны системы пружин – будет как раз и равна изменению действующих сил: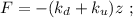
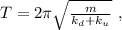 где
где 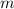 – масса шарика.
– масса шарика.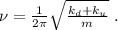
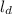 (нижней), и
(нижней), и 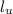 (верхней). При этом положим вертикальное положение груза
(верхней). При этом положим вертикальное положение груза  Ось
Ось 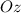 направлена вверх.
направлена вверх.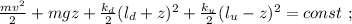
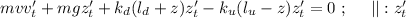
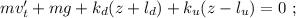
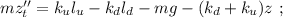
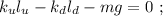
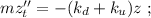
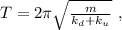 где
где 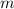 – масса шарика.
– масса шарика.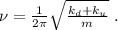
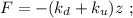
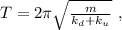 где
где 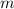 – масса шарика.
– масса шарика.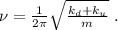
 Н/см
Н/см 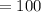 Н
Н 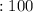 см
см 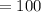 Н
Н 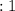 м
м 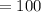 Н/м ;
Н/м ;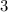 Н/см
Н/см 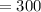 Н
Н 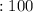 см
см 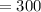 Н
Н 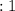 м
м 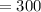 Н/м ;
Н/м ;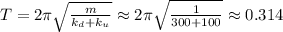 сек ;
сек ;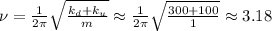 Гц .
Гц .
Легко понять, что множество таких возможных векторов скорости ветра
Аналогично можно понять, что множество тех же возможных векторов скорости ветра
Откуда видно, что максимальная скорость ветра
Гипотенуза
Двойная площадь этого треугольника равна:
С другой стороны двойная площадь этого треугольника равна произведению гипотенузы на половину искомого вектора максимальной скорости ветра (являющуюся высотой к гипотенузе):
Угол между баржей и максимальным ветром найдём из того же прямоугольного треугольника, через угол между красным катетом и высотой, который из подобия равен углу между векторами
1)
2)