1.5 Обозначим скорость движения второго велосипедиста: v₂ км/ч,
скорость первого велосипедиста: v₁ км/ч,
скорость первого велосипедиста пешком: v км/ч.
По условию: v₁ = 4v
Тогда время движения первого велосипедиста:
t₁ = S₁/v₁ + S₂/v = 2/(4v) + 4/v (ч)
Время движения второго велосипедиста:
t₂ = (S₁+S₂)/v₂ (ч)
По условию: t₁ = t₂. Тогда:
2/(4v) + 4/v = 6/v₂
1/(2v) + 8/(2v) = 6/v₂
9v₂ = 12v = 3v₁ => v₁/v₂ = 9/3 = 3
ответ: Скорость езды первого велосипедиста больше, чем скорость второго в 3 раза.
1.6 Для более понятной записи обозначим расстояние, оставшееся после дождя до дома бабушки за S₃, а расчетную скорость движения за v.
Все расстояние обозначим S. Красная Шапочка (КШ) планировала пройти это расстояние со скоростью v за время t.
Вместо этого со скоростью v за время t₁ КШ только расстояние S₁ до начала дождя.
Затем какое-то время t₂, пока шел дождь, КШ двигалась со скоростью v₂, меньше расчетной, и расстояние S₂.
После этого оставшееся расстояние S₃ она со скоростью v₃, больше расчетной, за время t₃.
Так как S = S₁+S₂+S₃ и t = t₁+t₂+t₃, то:
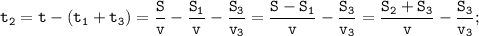
В вопросе заданы только скорости - найти нужно тоже только скорости. Значит расстояние в этой задаче можно взять любым числом удобным для расчетов. Для этой задачи очень удобное число для расстояния 144 км - оно и на 8 и на 9 и на 16 делится .
Тогда все просто.
Полпути 72 км.
Время в пути 144/16 = 9 часов. Раз первую половину ехал в 8 раз быстрее- значит и времени затратил в 8 раз меньше. Полпути час , вторую половину 8 часов - всего 9 и получается.
Скорость на первой половине 72/ 1 = 72 км/час , на второй 72/8 = 9 км/ час .
Половина времени 4.5 часа. Из них первый час 72 км , последующие 3.5 часа - 3.5* 9 = 31.5 км.
Всего за первую половину времени 72+31.5 = 103.5 км за 4.5 часа . Средняя скорость за первую половину времени 103.5/ 4.5 = 23 км/ час