Небольшое тело массой м лежит на поверхности гладкой полусферы радиусом r. в тело попадает пуля массой m, летящая горризонтально, и застревает в нем. пренебрегая смещением тела во время удара, определить при какой минимальной скорости пули тело сразу оторвется от поверхности полусферы?
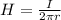
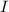 сила тока
сила тока  расстояние от проводника в данной задаче на середине наикратчайшего расстояния
расстояние от проводника в данной задаче на середине наикратчайшего расстояния 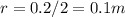
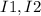
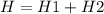
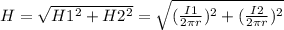
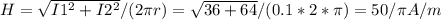 ответ
ответ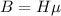
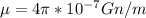
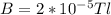 ответ
ответ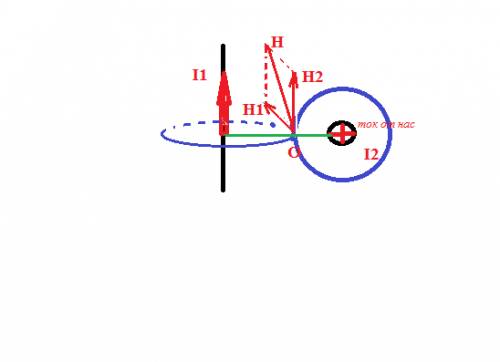
mp⋅υp = (m + mp)⋅υ0, υp = (m + mp)⋅υ0/mp