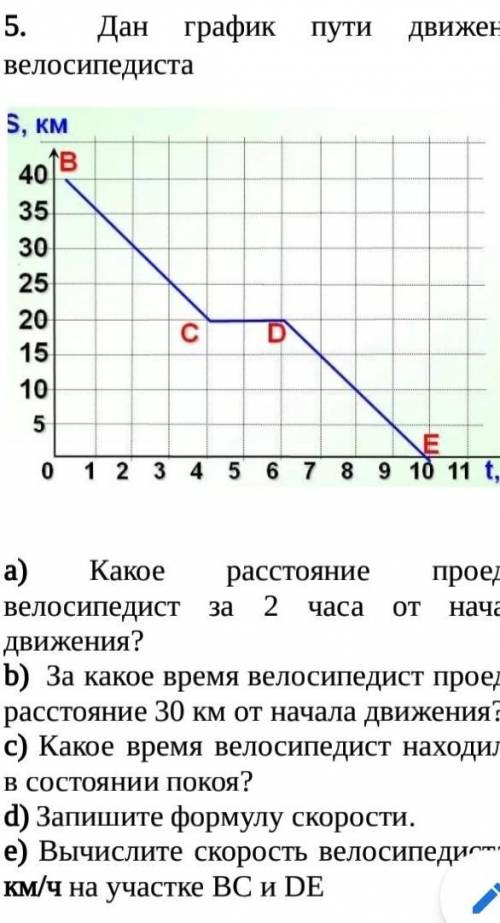
ответ:Ток течет от плюса к минусу
Объяснение:
Ток течет от плюса к минусу. Так принято считать. На самом деле двигаются электроны(минус). Т.к. ток течет от плюса к минусу. По правилу обхвата определяем полюса катушки с током. По правилу Ленца (возникающий в замкнутом контуре индукционный ток направлен таким образом, что его магнитное поле противодействует магнитному потоку которым он был вызван.) Определяем полюса катушки с индукционным током. По правилу обхвата определяем направление индукционного тока. Чертёж внизу
Дано: m(в) = 3 кг
t₁(в) = 20°С
m(с) = 0,2 кг
t₁(с) = 400°С
Найти: t₂(в) - ?
Теплоемкость воды равна 4200 Дж/(кг*град)
Теплоемкость стали равна 500 Дж/(кг*град)
Так как в конечном итоге температуры стали и воды выравняются, обозначим эту температуру через х.
Если пренебречь потерями, то количество теплоты которое отдала стальная деталь равна количеству теплоту, которая была принята водой, поэтому можно записать:
Q = c(в) * m(в) * (х - t₁(в)) = c(с) * m(с) * (t₁(с) - х)
4200 * 3 * (х - 20) = 500 * 0,2 * (400 - х)
12600х - 252000 = 40000 - 100х
12700 х = 292000
х = 23
ответ: до температуры 23°С
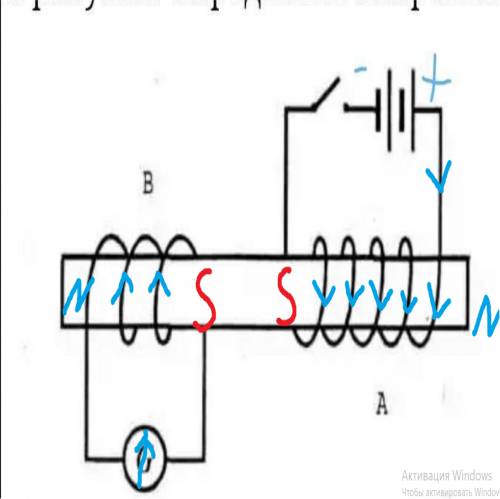
a). Расстояние, которое проедет велосипедист за 2 часа от начала движения (красный участок рис. 1):
S₁ = 30 - 40 = -10 (км)
Знак минус показывает, что перемещение велосипедиста направлено против выбранного направления на оси координат. Другими словами, велосипедист возвращается в точку начала отсчета..))
b). Перемещение велосипедиста на 30 км при начале движения от точки 40 км, очевидно, будет на отметке 10 км:
S₂ = 10 - 40 = -30 (км) (серая линия вдоль оси S рис.2)
Находим на графике точку пути, соответствующую 10 км отметке (желтая линия), и опускаем перпендикуляр (красная линия) на ось времени t.
30 км от начала движения велосипедист проедет за 8 часов.
c). В состоянии покоя (на отметке 20 км) велосипедист находился 2 часа, - с 4 до 6 часов после начала движения. Перемещение велосипедиста на промежутке CD равно нулю.
d-е). Скорость велосипедиста в процессе движения на участке ВС:
v = S(bc) : t(bc) = 20 : 4 = 5 (км/ч)
Эту же скорость можно получить на участке DE:
v = S(de) : t(de) = 20 : 4 = 5 (км/ч)
Средняя скорость движения велосипедиста на всем пути:
v(cp.) = S : t = 40 : 10 = 4 (км/ч)