молекулы воздуха движутся и потому непрерывно ударяют о стенки шарика внутри и снаружи. При откачивании воздуха число молекул под колоколом вокруг оболочки шарика уменьшается. Но внутри завязанного шарика их число не изменяется. Поэтому число ударов молекул о внешнюю поверхность оболочки становится меньше числа ударов о внутреннюю поверхность. Из-за этого шарик раздувается и принимает такие размеры, при которых сила упругости его резиновой оболочки становится равной силе давления газа, находящегося внутри его.
Сферическая форма, которую принимает раздутая оболочка шарика показывает, что газ оказывает по всем направлениям одинаковое давление.
Выясним, как зависит давление газа от его объема. Температуру газа будем считать постоянной.
Если объем газа уменьшить, но так, чтобы масса его осталась неизменной, то в каждом кубическом сантиметре газа молекул станет больше. Это означает, что плотность газа увеличится. Тогда число ударов молекул о стенки сосуда возрастет и давление газа станет больше.
итог, давление воздуха, зависит не только от массы.
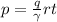
где, p давление
q давление
гамма - количество
r- газ.постоянная
t - температура
допустим, t постоянно, как и собственно r.
тогда, давление прямо пропорционально давлению и обратно пропорционально количеству вещества.
а здесь думаю станет всё ясно.
PS: за формулы сорри, приложение не позволяет пользоваться греческими символами, и заглавными тоже. вопрос, задачи по математике и физике без этого ? интересно, разрабы об этом не подумали?!
Графическое изображение зависимости между напряжениями (или нагрузками) и деформациями материала (или перемещениями при деформировании) представляет собой диаграмму деформирования.
Испытательные машины имеют специальные при которые автоматически фиксируют диаграмму растяжения. На диаграмме по оси ординат откладываются действующие осевые нагрузки, а по оси абсцисс — абсолютные деформации.
На рис. 2.2 даны типичные диаграммы растяжения различных металлов. Диаграмма с постепенным переходом из упругой в пластическую область (рис. 2.2, а) свойственна большинству металлов в пластичном состоянии (легированные стали, медь, бронза).
Диаграммы растяжения
Рис. 2.2. Диаграммы растяжения:
а — для большинства металлов в пластичном состоянии с постепенным переходом из упругой в пластическую область; б — для некоторых металлов в пластичном состоянии со скачкообразным переходом в пластическую область; в — для хрупких металлов
Пластичные материалы разрушаются при больших остаточных деформациях (больших остаточных удлинениях, измеряемых после разрыва).
Диаграмма со скачкообразным переходом в пластическую область в виде четко обозначенной «площадки» текучести (рис. 2.2, б) свойственна некоторым металлам. К таким металлам можно отнести мягкую углеродистую сталь, а также некоторые отожженные марганцовистые и алюминиевые бронзы.
Хрупкие материалы разрушаются при малых остаточных деформациях. К хрупким материалам можно отнести закаленную и неотпущенную сталь, серый чугун.
Характерные участки и точки диаграммы растяжения показаны на рис. 2.3. По оси абсцисс откладывают абсолютные удлинения А/ образца, а по оси ординат — значения растягивающей силы Р. Сначала получим на первом участке диаграммы 0—1 прямолинейную зависимость между силой и удлинением, что отражает закон Гука. При дальнейшем увеличении силы (за точкой 1) прямолинейная зависимость между Р и А/ нарушается. Точка 1 соответствует пределу пропорциональности, т. е. наибольшему напряжению, при котором еще соблюдается закон Гука. Если нагрузку, соответствующую точке 1, обозначить ,Pnu, а начальную площадь сечения образца Fq, то предел пропорциональности Характерные участки и точки диаграммы растяжения
Объяснение:
На нагрев воды от 0 до 100 градусов требуется Q1=cm(t2-t1)=0,1*4200*(100-10)=37800 Дж
На испарение воды затратилось 200000-37800=162200 Дж
Тогда испарилось воды m=Q/r=162200/2*10⁶=0,081 кг≈ 81 г