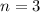Согласно теории Бора на электрон который движется вокруг полностью ионизированного атомного ядра водорода, в состав которого входит лишь протон (другими словами просто вокруг протона), по четкой, стационарной, орбите, номером и радиусом , центробежная сила действующая на электрон (в его СО(которую нельзя назвать инерциальной)) будет равна силе кулоновского взаимодействия между электронном и протоном.
Отсюда
Так как , то
Т.к. при , то , отсюда
⇒ ⇒ (1)
Согласно правилу квантовых орбит (из всё той же теории Бора)
Значит, рассмотрим время движения, а потом сложим. Время затрачено на: 1. Ракета движется вертикально вверх с ускорением 20 сек; 2. Ракета движется равнозамедленно, т.к. двигатели отключили именно с этого момента. Время ушло на потерю всей скорости направленную вертикально вверх; 3. Ракета потеряла всю скорость, и теперь она падает с ускорением свободного падения. Решение: 1. t₁=20 сек, после отключения двигателей он имеет v=at=20*8=160 м/с 2. v-gt₂=0 => t₂=v/g=160/10= 16 сек 3.Время на падение найдём через высоту на которую он взлетел. Сначала он двигался с ускорением, т.е. h₁=at₁²/2=8*400/2=1600 м После, без ускорения, с набравшейся скоростью движется вертикально вверх h₂=vt₂-gt₂²/2=160*16 - 10*16²/2= 1280 м h=h₁+h₂=2880 м И так ищем время направленное на падение: h=gt₃²/2 => t₃=√2h/g = √2*2880/10=24 сек. Осталось сложить: t=t₁+t₂+t₃=20+16+24=60 сек.
ответ: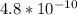 м
м
Объяснение:
Дано:
-----------
Согласно теории Бора на электрон который движется вокруг полностью ионизированного атомного ядра водорода, в состав которого входит лишь протон (другими словами просто вокруг протона), по четкой, стационарной, орбите, номером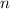 и радиусом
и радиусом 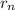 , центробежная сила
, центробежная сила 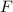 действующая на электрон (в его СО(которую нельзя назвать инерциальной)) будет равна силе кулоновского взаимодействия
действующая на электрон (в его СО(которую нельзя назвать инерциальной)) будет равна силе кулоновского взаимодействия 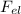 между электронном и протоном.
между электронном и протоном.
Отсюда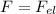
Так как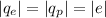 , то
, то 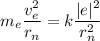
Т.к.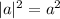 при
при 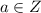 , то
, то  , отсюда
, отсюда
Согласно правилу квантовых орбит (из всё той же теории Бора)
Прививая уравнения (1) и (2) получим
При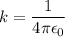
Отсюда, при