Железнодорожная платформа движется со скоростью 11 км/ч. Из орудия, закреплённого на платформе, производится выстрел в направлении против движения платформы. Масса снаряда — 21 кг, его скорость — 627 м/с. Масса платформы с орудием — 23 т. Определи скорость платформы после выстрела.

👇

Открыть все ответы

Ответ:

doagetonya

26.05.2020

1. Тело свободно падает с высоты 39,2 м. За какое время тело пройдет: а) первый метр своего пути; б) последний метр своего пути? Чему равна средняя скорость на второй половине пути?

Дано:

h = 39{,}2 м

$v_{0}=0$

g = 10 м/с²

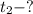
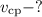
Найти: а) $t_{1}-?$ б) $t_{2}-?$ $v_{\text{cp}}-?$

Решение. а) Следует определить время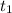 $t_{1}$ , за которое тело пройдет расстояние, равное 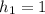$h_{1} = 1$ м.

Направим ось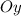 в сторону падения тела. Воспользуемся формулой:

$h_{y} = v_{0y}t + \dfrac{g_{y}t^{2}}{2}$

Перейдем от проекций к модулям:

$h_{1y}=h_{1}$

$v_{0y}=v_{0}=0$

$g_{y} = g$

Тогда $h_{1} = \dfrac{gt^{2}_{1}}{2} \Rightarrow t_{1} = \sqrt{\dfrac{2h_{1}}{g} }$

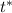б) Время $t^{*}$ , за которое тело пройдет расстояние, равное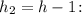 $h_{2} = h-1 \colon$

$t^{*} = \sqrt{\dfrac{2h_{2}}{g} } = \sqrt{\dfrac{2(h-1)}{g} }$

Полное время: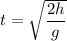 $t = \sqrt{\dfrac{2h}{g} }$

Тогда последний метр своего пути тело пройдет за: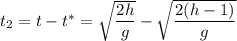 $t_{2} = t - t^{*} =\sqrt{\dfrac{2h}{g} } - \sqrt{\dfrac{2(h-1)}{g} }$

Следует определить среднюю скорость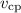 $v_{\text{cp}}$ на второй половине пути.

Длина первой половины пути –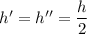 $h'= h'' = \dfrac{h}{2}$

Тогда можно записать, что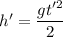 $h' = \dfrac{gt'^{2}}{2}$ , где 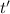– время прохождения телом первой половины пути, его можно найти: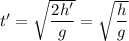 $t' = \sqrt{\dfrac{2h'}{g} } = \sqrt{\dfrac{h}{g} }$

Тогда время на второй половине пути: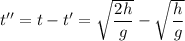 $t'' = t - t' = \sqrt{\dfrac{2h}{g} } - \sqrt{\dfrac{h}{g} }$

Чтобы определить среднюю путевую скорость, нужно разделить весь путь на все время:

$v_{\text{cp}} = \dfrac{h''}{t''} = \dfrac{\dfrac{h}{2} }{\sqrt{\dfrac{2h}{g} } - \sqrt{\dfrac{h}{g} }}$

Определим значение искомых величин:

а)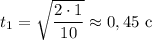 $t_{1} = \sqrt{\dfrac{2 \cdot 1}{10} } \approx 0,45 \ \text{c}$

б)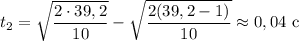 $t_{2} = \sqrt{\dfrac{2 \cdot 39,2}{10} } - \sqrt{\dfrac{2 (39,2 - 1)}{10} } \approx 0,04 \ \text{c}$

$v_{\text{cp}} = \dfrac{\dfrac{39{,}2}{2} }{\sqrt{\dfrac{2 \cdot 39{,}2}{10} } - \sqrt{\dfrac{39{,}2}{10} }} \approx 24$ м/с

ответ: а) 0,45 с; б) 0,04 с; 24 м/с.

2. Тело, которое свободно падает без начальной скорости, за последнюю секунду движения проходит $\dfrac{2}{3}$ всего пути. Определите путь, пройденный телом за время падения.

Дано:

$v_{0} = 0$

$h' = \dfrac{2}{3} h$

g = 10 м/с²

Найти: h-?

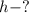
Решение. Высота падения тела: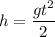 $h = \dfrac{gt^{2}}{2}$

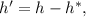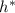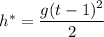
Тогда путь $h' = h - h^{*},$ где $h^{*}$ – путь, пройденный за время (t - 1) , то есть $h^{*} = \dfrac{g(t-1)^{2}}{2}$

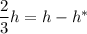
Тогда $\dfrac{2}{3} h = h - h^{*}$

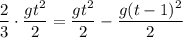
Имеем: $\dfrac{2}{3} \cdot \dfrac{gt^{2}}{2} = \dfrac{gt^{2}}{2} -\dfrac{g(t-1)^{2}}{2}$

Сократим обе части уравнения на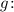 $g \colon$

$\dfrac{t^{2}}{3} = \dfrac{t^{2} - (t-1)^{2}}{2}$

$\dfrac{t^{3}}{3} = \dfrac{2t - 1}{2}$

$2t^{2} = 3(2t -1)$

$2t^{2} - 6t + 3 = 0$

$D = (-6)^{2} - 4 \cdot 2 \cdot 3 = 12$

$t_{1} = \dfrac{6 + 2\sqrt{3}}{4} \approx 2,37 \ \text{c}$

$t_{2} = \dfrac{6 - 2\sqrt{3}}{4} \approx 0,63 < 1$

Таким образом, тело весь путь за 2,37 с. Тогда

$h = \dfrac{10\cdot (2,37)^{2}}{2} \approx 28$ м

ответ: 28 м.

3. Тело свободно падает с высоты 60 м. Определите его перемещение за последнюю секунду падения.

Дано:

h = 60 м

g = 10 м/с²

Найти: h'-?

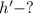
Решение. Полное время: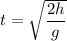 $t = \sqrt{\dfrac{2h}{g} }$

Пройденный путь тела за (t - 1) секунд:

$h^{*} = \dfrac{g(t-1)^{2}}{2} = \dfrac{g\left(\sqrt{\dfrac{2h}{g} }-1\right)^{2}}{2}$

Имеем:

$h' = h - h^{*} = h - \dfrac{g\left(\sqrt{\dfrac{2h}{g} }-1\right)^{2}}{2}$

Определим значение искомой величины:

$h' = 60 - \dfrac{10 \cdot \left(\sqrt{\dfrac{2\cdot 60}{10} }-1\right)^{2}}{2} \approx 30$ м

ответ: 30 м.

4,8(43 оценок)

Ответ:

4ae444ka

26.05.2020

Что происходит? Сама кастрюля, вместе с краской нагревается в непосредственном контакте с водой, и поэтому цвет кастрюли не имеет никакого значения. После того, как кастрюли выставили в это "холодное место" (правда жуть?) . Нет, тут надо остановиться. Под этим термином, надеюсь, подразумевается, что там нет источников энергии излучающих интенсивный свет и инфракрасное излучение. Итак, в холодном месте материал кастрюли и краски на ней начинает остывать передавая часть (большую часть) тепла воздуху при непосредственном контакте и за счет излучения инфракрасных волн. Так как излучает, а не поглощает, цвет кастрюли не имеет значения и в этом случае. ответ, одинаковые кастрюли, с одинаковой температурой и одинаковым количеством воды остынут одинаково. Вот если бы их выставили на солнечный свет, я бы сказал, что черная кастрюля остыла бы медленнее, потому что черный цвет потому и черный, что поглощает почти полностью видимый свет всего диапазона спектра вместе и их энергией.

4,8(37 оценок)

Это интересно:

Компьютеры-и-электроника

10.04.2023

Как сделать пользователя администратором в групповом чате Skype на ПК или Mac...

Образование-и-коммуникации

27.05.2021

Как сделать так, чтобы лед долго не таял...

Компьютеры-и-электроника

11.10.2022

Как легко и удобно пользоваться Apple TV...

Здоровье