Задача №4 На графике изображен процесс теплообмена. Какие вещества (тела) участвуют в теплообмене? Объясните значение отдельных участков графика. Почему участок КМ изображен пунктиром? Задача №5 По графику определите: Какие вещества участвовали в теплообмене? Изменялось ли агрегатное состояние веществ? Придумайте свою задачу.
1. Тело свободно падает с высоты 39,2 м. За какое время тело пройдет: а) первый метр своего пути; б) последний метр своего пути? Чему равна средняя скорость на второй половине пути?
Дано:
м
м/с²
Найти: а) б)
Решение. а) Следует определить время , за которое тело пройдет расстояние, равное м.
Направим ось в сторону падения тела. Воспользуемся формулой:
Перейдем от проекций к модулям:
Тогда
б) Время , за которое тело пройдет расстояние, равное
Полное время:
Тогда последний метр своего пути тело пройдет за:
Следует определить среднюю скорость на второй половине пути.
Длина первой половины пути –
Тогда можно записать, что , где – время прохождения телом первой половины пути, его можно найти:
Тогда время на второй половине пути:
Чтобы определить среднюю путевую скорость, нужно разделить весь путь на все время:
Определим значение искомых величин:
а)
б)
м/с
ответ: а) 0,45 с; б) 0,04 с; 24 м/с.
2. Тело, которое свободно падает без начальной скорости, за последнюю секунду движения проходит всего пути. Определите путь, пройденный телом за время падения.
Дано:
м/с²
Найти:
Решение. Высота падения тела:
Тогда путь где – путь, пройденный за время , то есть
Тогда
Имеем:
Сократим обе части уравнения на
Таким образом, тело весь путь за 2,37 с. Тогда
м
ответ: 28 м.
3. Тело свободно падает с высоты 60 м. Определите его перемещение за последнюю секунду падения.
Спина прямая, руки на поясе. Дети плавно и медленно поднимают то правую, то левую ногу, согнутую в колене, и также плавно опускают. Следить за спиной.) — Аист, аист длинноногий, Покажи домой дорогу. (Аист отвечает.) — Топай правою ногою, Топай левою ногою, Снова — правою ногою, Снова — левою ногою. После — правою ногою, После — левою ногою. И тогда придешь домой. А над морем — мы с тобою! Над волнами чайки кружат, Полетим за ними дружно. Брызги пены, шум прибоя, А над морем — мы с тобою! (Дети машут руками, словно крыльями.) Мы теперь плывём по морю И резвимся на просторе. Веселее загребай И дельфинов догоняй. (Дети делают плавательные движения руками.) А сейчас мы с вами, дети А сейчас мы с вами, дети, Улетаем на ракете. На носки поднимись, А потом руки вниз. Раз, два, три, четыре — Вот летит ракета ввысь! (1—2 — стойка на носках, руки вверх, ладони образуют «купол ракеты»; 3—4 — основная стойка.) А теперь на месте шаг А теперь на месте шаг. Выше ноги! Стой, раз, два! (Ходьба на месте.) Плечи выше поднимаем, А потом их опускаем. (Поднимать и опускать плечи.) Руки перед грудью ставим И рывки мы выполняем. (Руки перед грудью, рывки руками.) Десять раз подпрыгнуть нужно, Скачем выше, скачем дружно! (Прыжки на месте.) Мы колени поднимаем — Шаг на месте выполняем. (Ходьба на месте.) От души мы потянулись, (Потягивания — руки вверх и в стороны.) И на место вновь вернулись. (Дети садятся.)
1. Тело свободно падает с высоты 39,2 м. За какое время тело пройдет: а) первый метр своего пути; б) последний метр своего пути? Чему равна средняя скорость на второй половине пути?
Дано:
Найти: а) б)
б) 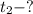
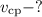
Решение. а) Следует определить время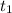 , за которое тело пройдет расстояние, равное
, за которое тело пройдет расстояние, равное 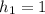 м.
м.
Направим ось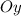 в сторону падения тела. Воспользуемся формулой:
в сторону падения тела. Воспользуемся формулой:
Перейдем от проекций к модулям:
Тогда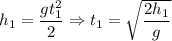
б) Время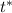 , за которое тело пройдет расстояние, равное
, за которое тело пройдет расстояние, равное 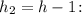
Полное время: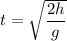
Тогда последний метр своего пути тело пройдет за: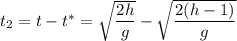
Следует определить среднюю скорость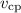 на второй половине пути.
на второй половине пути.
Длина первой половины пути –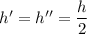
Тогда можно записать, что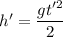 , где
, где 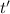 – время прохождения телом первой половины пути, его можно найти:
– время прохождения телом первой половины пути, его можно найти: 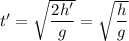
Тогда время на второй половине пути: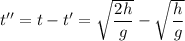
Чтобы определить среднюю путевую скорость, нужно разделить весь путь на все время:
Определим значение искомых величин:
а)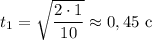
б)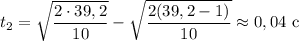
ответ: а) 0,45 с; б) 0,04 с; 24 м/с.
2. Тело, которое свободно падает без начальной скорости, за последнюю секунду движения проходит всего пути. Определите путь, пройденный телом за время падения.
всего пути. Определите путь, пройденный телом за время падения.
Дано:
Найти: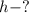
Решение. Высота падения тела: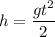
Тогда путь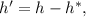 где
где 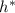 – путь, пройденный за время
– путь, пройденный за время  , то есть
, то есть 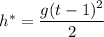
Тогда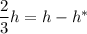
Имеем: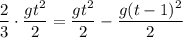
Сократим обе части уравнения на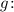
Таким образом, тело весь путь за 2,37 с. Тогда
ответ: 28 м.
3. Тело свободно падает с высоты 60 м. Определите его перемещение за последнюю секунду падения.
Дано:
Найти: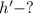
Решение. Полное время: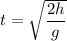
Пройденный путь тела за секунд:
секунд:
Имеем:
Определим значение искомой величины:
ответ: 30 м.