Question

Два медных шарика столкнулись на гладкой поверхности. Радиус первого шарика в 3 раза больше радиуса второго шарика. С точностью до сотых определи отношение ускорений 12, приобретённых шариками во время удара, (1 — ускорение первого шарика, 2 — ускорение второго шарика).

Answer 1

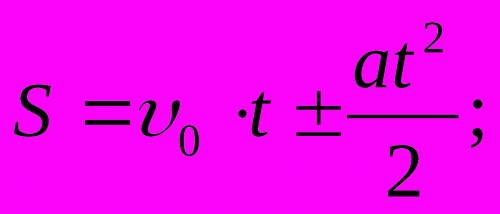
ответ:8

Объяснение:

Примем R1=1x за радиус первого шара, R2=2x за радиус второго шара. Ускорение можно найти по формуле a=\frac{F}{m} (ускорение равно сила деленная на массу). Сила у обоих тел будет одинакова по 3 закону Ньютона. В свою очередь, массу можно найти по формуле m=p*V (масса равна произведению плотности и объема). Плотность у обоих тел будет одинакова, так как они сделаны из одного материала.

А V=\frac{4}{3}*\pi*R^{3}(Объем равен \frac{4}{3}"пи" на радиус в кубе). Так как "пи" является константой, мы можем отбросить эту переменную в конечном уравнении, как и другие равные для обоих тел значения, и получим: \frac{m_{1}}{m_{2}}=\frac{R^{3}_{1}}{R^{3}_{2}}=\frac{1^{3}}{2^{3}}=\frac{1}{8}. Из этого выходит, что масса первого тела в 8 раз МЕНЬШЕ массы второго. И, согласно этой информации, мы по формуле (a=\frac{F}{m}) можем вычислить, что ускорение первого тела в 8 БОЛЬШЕ ускорения второго тела. Таким образом: \frac{8}{1}=8.