Объяснение:
Задачи на плотность, массу и объем с решением
Формулы, используемые в задачах по физике на плотность, массу и объем.
Название величины
Обозначение
Единицы измерения
Формула
Масса
m
кг
m = p * V
Объем
V
м3
V = m / p
Плотность
p
кг/м3
p = m / V
Плотность равна отношению массы тела к его объёму. Плотность обозначают греческой буквой ρ (ро).
Значок
Физика 7 класс: все формулы и определения КРУПНО на трех страницах
1 файл(ы) 255.55 KB
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1. Найдите плотность молока, если 206 г молока занимают объем 200 см3?
задача 4
Задача № 2. Определите объем кирпича, если его масса 5 кг?
задача 5
Задача № 3. Определите массу стальной детали объёмом 120 см3
задача 6
Задача № 4. Размеры двух прямоугольных плиток одинаковы. Какая из них имеет большую массу, если одна плитка чугунная, другая — стальная?
Решение: Из таблицы плотности веществ (см. в конце страницы) определим, что плотность чугуна (ρ2 = 7000 кг/м3) меньше плотности стали (ρ1 = 7800 кг/м3). Следовательно, в единице объема чугуна содержится меньшая масса, чем в единице объема стали, так как чем меньше плотность вещества, тем меньше его масса, если объемы тел одинаковы.
Задача № 5. Определите плотность мела, если масса его куска объемом 20 см3 равна 48 г. Выразите эту плотность в кг/м3 и в г/см3.
ответ: Плотность мела 2,4 г/см3, или 2400 кг/м3.
Задача № 6. Какова масса дубовой балки длиной 5 м и площадью поперечного сечения 0,04 м2 ?
ОТВЕТ: 160 кг.
РЕШЕНИЕ. Из формулы для плотности получаем m = p • V. С учетом того, что объем балки V = S • l , получаем: m = p • S • l.
Вычисляем: m = 800 кг/м3 • 0,04 м2 • 5 м = 160 кг.
Задача № 7. Брусок, масса которого 21,6 г, имеет размеры 4 х 2,5 х 0,8 см. Определить, из какого вещества он сделан.
ОТВЕТ: Брусок сделан из алюминия.
Задача № 8 (повышенной сложности). Полый медный куб с длиной ребра а = 6 см имеет массу m = 810 г. Какова толщина стенок куба?
ОТВЕТ: 5 мм.
РЕШЕНИЕ: Объем кубика VK = а3 = 216 см3. Объем стенок VС можно вычислить, зная массу кубика mК и плотность меди р: VС = mК / р = 91 см3. Следовательно, объем полости VП = VK — VC = 125 см3. Поскольку 125 см3 = (5 см)3, полость является кубом с длиной ребра b = 5 см. Отсюда следует, что толщина стенок куба равна (а — b)/2 = (6 – 5)/2 = 0,5 см.
Задача № 9 (олимпиадный уровень). Масса пробирки с водой составляет 50 г. Масса этой же пробирки, заполненной водой, но с куском металла в ней массой 12 г составляет 60,5 г. Определите плотность металла, помещенного в пробирку.
ОТВЕТ: 8000 кг/м3
РЕШЕНИЕ: Если бы часть воды из пробирки не вылилась, то в этом случае общая масса пробирки, воды и куска металла в ней была бы равна 50 г + 12 г = 62 г. По условию задачи масса воды в пробирке с куском металла в ней равна 60,5 г. Следовательно, масса воды, вытесненной металлом, равна 1,5 г, т. е. составляет 1/8 массы куска металла. Таким образом, плотность металла в 8 раз больше плотности воды.
Задачи на плотность, массу и объем с решением. Таблица плотности веществ.
Задачи на плотность
Справочный материал для «Задачи на плотность, массу и объем«
Задачи на плотность, массу и объем с решением
Как, зная только массу, рассчитать плотность?
Если объем тела (вещества) неизвестен или не задан явно в условиях задачи, то попытайтесь его измерить, вычислить или узнать, используя косвенные (дополнительные) данные.
Если вещество сыпучее или жидкое, то оно, как правило, находится в емкости, которая обычно имеет стандартный объем. Так, например, объем бочки обычно равен 200 литров, объем ведра – 10 литров, объем стакана – 200 миллилитров (0,2 литра), объем столовой ложки – 20 мл, объем чайной – 5 мл. Об объеме трехлитровых и литровых банок нетрудно догадаться из их названия.
1. Ускорение - физическая величина, определяющая быстроту изменения скорости тела.
2. Неравномерное движение - движение, при котором тело проходит разный путь за определённый промежуток времени.
3. Траектория - линия, по которой движется тело. Траектория бывает прямолинейной --- и криволинейной ~~~
4. 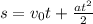
5. Материальная точка - точка, имеющая массу. Её размерами в условиях решаемой задачи можно пренебречь.
Материальной точкой можно считать автомобиль, который км; футболиста, который бежит от центра поля к воротам противника; самолёт, совершающий рейс из Москвы в Санкт-Петербург.
Информационный баннер
Физика для "чайников"
Задачи на тему «Сила упругости. Закон Гука» с решениями
Иван
Иван
28 Май 2019
39 169
Время чтения: 8 минут
Доверь свою работу кандидату наук!
Примеры работ
Узнать стоимость
Содержание
Сила упругости и закон Гука: определения
Вопросы на силу упругости и закон Гука
Задачи на силу упругости и закон Гука с решениями
Задача №1. Расчет силы упругости
Задача №2. Нахождение жесткости пружины
Задача №3. Нахождение ускорения тела
Задача №4. Нахождение жесткости пружины по графику
Задача №5. Определение энергии деформации
Можно не знать закон Ома и сидеть дома. Но если не знаешь закон Гука – лучше тоже не выходить. Особенно, если идешь на экзамен по физике.
Здесь устраняем пробелы в знаниях и разбираемся, как решать задачи на силу упругости и применение закона Гука. А за полезной рассылкой для студентов добро на наш телеграм-канал.
Сила упругости и закон Гука: определения
Сила упругости – сила, препятствующая деформациям и стремящаяся восстановить первоначальные форму и размеры тела.
Примеры действия силы упругости:
пружины сжимаются и разжимаются в матрасе;
мокрое белье колышется на натянутой веревке;
лучник натягивает тетиву, чтобы выпустить стрелу.
Простейшие деформации – деформации растяжения и сжатия.
Закон Гука:
Деформация, возникающая в упругом теле под действием внешней силы, пропорциональна величине этой силы.
Коэффициент k – жесткость материала.
Есть и другая формулировка закона Гука. Введем понятие относительной деформации «эпсилон» и напряжения материала «сигма»:
S – площадь поперечного сечения деформируемого тела. Тогда закон Гука запишется так: относительная деформация пропорциональна напряжению.
Здесь Е – модуль Юнга, зависящий от свойств материала.
Закон Гука был экспериментально открыт в 1660 году англичанином Робертом Гуком.
Вопросы на силу упругости и закон Гука
Вопрос 1. Какие бывают деформации?
ответ. Помимо простейших деформаций растяжения и сжатия, бывают сложные деформации кручения и изгиба. Также разделяют обратимые и необратимые деформации.
Вопрос 2. В каких случаях закон Гука справедлив для упругих стержней?
ответ. Для упругих стержней (в отличие от эластичных тел) закон Гука можно применять при малых деформациях, когда величина эпсилон не превышает 1%. При больших деформациях возникают явления текучести и необратимого разрушения материала.
Вопрос 3. Как направлена сила упругости?
ответ. Сила упругости направлена в сторону, противоположную направлению перемещения частиц тела при деформации.
Вопрос 4. Какую природу имеет сила упругости?
ответ. Сила упругости, как и сила трения – электромагнитная сила. Она возникает вследствие взаимодействия между частицами деформируемого тела.
Вопрос 5. От чего зависит коэффициент жесткости k? Модуль Юнга E?
ответ. Коэффициент жесткости зависит от материала тела, а также его формы и размеров. Модуль Юнга зависит только от свойств материала тела.
Задачи на силу упругости и закон Гука с решениями
Кстати! Для наших читателей действует скидка 10% на любой вид работы.
Задача №1. Расчет силы упругости
Условие
Один конец проволоки жестко закреплен. С какой силой нужно тянуть за второй конец, чтобы растянуть проволоку на 5 мм? Жесткость проволоки известна и равна 2*10^6 Н/м2.
Решение
Запишем закон Гука:
По третьему закону Ньютона:
ответ: 10 кН.