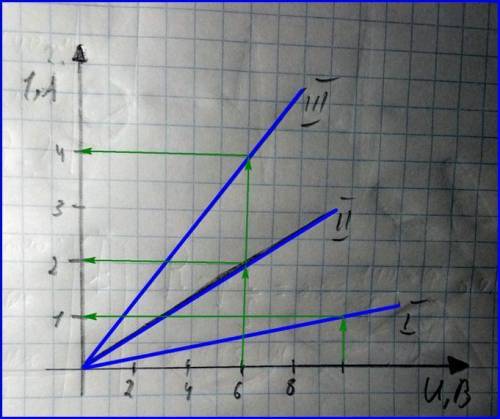
Выбираем на Вольт-Амперных Характеристиках (ВАХ)
удобные для расчётов значения напряжения и тока.
По формуле закона Ома вычисляем сопротивления
резисторов.
I.
U₁=10 B => I₁=1 A;
R₁=U₁/I₁=10/1=10 Ом.
II.
U₂=6 B => I₂=2 A;
R₂=U₂/I₂=6/2=3 Ом.
III.
U₃=6 B => I₃=4 A;
R₃=U₃/I₃=6/4=1,5 Ом.
Из вычисления видно, что:
R₁>R₂>R₃ при этом у токов
зависимость от сопротивления
резисторов обратная:
I₁<I₂<I₃.
Это полностью согласуется
с формулировкой закона Ома:
Сила тока в цепи прямо пропорциональна
напряжению на зажимах цепи и обратно
пропорциональна сопротивлению.
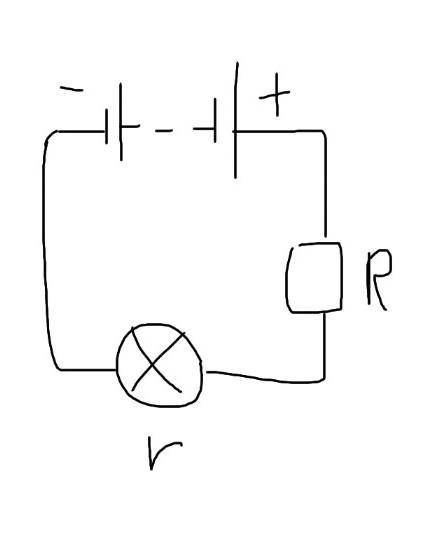
Дано:
r = 2 Ом
R = 4 Ом
N = 3
U = 1,5 В
n = 5%
Rmin, Rmax, Imin-Imax, Pmin, Pmax - ?
1) Найдём минимальное и максимальное значения сопротивления резистора:
Rmin = R*(1 - n/100) = R*(1 - 0,05) = R*0,95 = 4*0,95 = 3,8 Ом
Rmax = R*(1 + n/100) = R*(1 + 0,05) = R*1,05 = 4,2 Ом
2) Последовательно соединённые батарейки дают напряжение:
Uo = N*U = 3*1,5 = 4,5 В
Т.к. все элементы цепи соединены последовательно, a r = const, то найдём общее сопротивление цепи при Rmin и Rmax, чтобы найти диапазон значений силы тока (при последовательном соединении сила тока в цепи одинакова в любой её точке):
Ro(min) = r + Rmin = 2 + 3,8 = 5,8 Ом
Ro(max) = r + Rmax = 2 + 4,2 = 6,2 Ом
Imax = Uo/Ro(min) = 4,5/5,8 = 0,776 A = 776 мА
Imin = Uo/Ro(max) = 4,5/6,2 = 0,726 A = 726 мА
Номинал резистора +/-5% указывает на то, что значение сопротивления R может быть в пределах от 3,8 до 4,2 Ом, значит диапазон силы тока Imin-Imax будет в пределах от 726 до 776 мА.
3) P = I²*R
Для лампы:
Рmin = Imin²*r = 0,726²*2 = 1,05 Вт
Рmax = Imax²*r = 0,776²*2 = 1,2 Вт
ответ: 3,8 Ом, 4,2 Ом; от 726 мА до 776 мА; 1,05 Вт, 1,2 Вт.
где фото
Объяснение: