До ть з фізикою знайти силу натягу в момент коли кут між. мотузкою і вертикаллю становить 30 градусів

До ть з фізикою знайти силу натягу в момент коли кут між. мотузкою і вертикаллю становить 30 градусі

👇

Открыть все ответы

Ответ:

viktoriag373

04.03.2021

$h = \frac{ s }{ ( 1/ \mu - 1/ tg{\alpha} )( \cos{\alpha} - \mu \sin{\alpha} )^2 }$ , при условии: $arctg{(\mu)} < \alpha < arcCtg{(\mu)}$ ;

*** если же переход от наклонной плоскости скруглённый, и: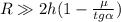 $R \gg 2h ( 1 - \frac{\mu}{tg{\alpha}} )$ , то:

$h = \frac{ s }{ 1/\mu - 1/tg{(\alpha)} }$ .

Объяснение:

По закону сохранений энергии:

$E_{ko} + E_{no} - A_\alpha = E_{k\alpha} + E_{n\alpha}$ ;

где:

$E_{ko} = 0$ и $E_{no} = mgh$ – начальные значения кинетической и потенциальной энергии;

$E_{k\alpha} = \frac{mv_\alpha^2}{2}$ и $E_{n\alpha} = 0$ – значения кинетической и потенциальной энергии перед ударом о горизонтальную поверхность, в самом низу наклонной плоскости;

$A_\alpha$ – работа силы трения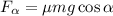 на наклонной плоскости;

$A_\alpha = F_\alpha \cdot L$ – работа

силы трения $F_\alpha = \mu mg \cos{\alpha}$ на наклонной плоскости,

где: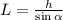 $L = \frac{h}{\sin{\alpha}}$ – длина наклонной плоскости;

$A_\alpha = \frac{ \mu mgh }{tg{\alpha}}$ ;

В итоге:

$mgh - \frac{ \mu mgh }{tg{\alpha}} = \frac{mv_\alpha^2}{2}$ ;

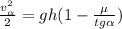(*) $\frac{v_\alpha^2}{2} = gh ( 1 - \frac{\mu}{tg{\alpha}} )$ ;

Из этого вытекает очевидное условие, что:

$1 - \frac{\mu}{tg{\alpha}} 0$ ;

$1 \frac{\mu}{tg{\alpha}}$ ;

$tg{\alpha} \mu$ , т.е. угол наклона должен быть более значения: $\alpha arctg{(\mu)}$ , иначе груз вообще не сдвинется с места, и, разумеется, никакого расстояния не пройдёт, а общая формула (данная в ответе) даст формально отрицательный ответ для высоты .

Теперь «удар», т.е. переход с наклонной плоскости на горизонталь. Во время удара теряется вертикальная составляющая импульса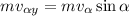 $mv_{\alpha y} = mv_\alpha \sin{\alpha}$ . Это происходит почти мгновенно ( 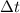$\Delta t$ ), под воздействием гасящей его чрезвычайно резко возрастающей на время гашения силы реакции опоры (и веса – соответственно) 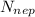$N_{nep}$ . Удар груза об опору в момент его перехода на горизонталь будем считать абсолютно неупругим, происходящим таким образом, что груз после него не подскакивает. Тогда можно записать, что:

$mv_{\alpha y} - N_{nep} \Delta t = 0$ ;

$N_{nep} = \frac{mv_{\alpha y}}{\Delta t}$ ;

За это время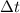 $\Delta t$ груз так же заметно замедляется под воздействием чрезвычайно резко возрастающей на время гашения силы трения:

$F_{nep} = \mu N_{nep} = \mu \cdot \frac{mv_{\alpha y}}{\Delta t}$ ;

Соответственно, гасится и горизонтальный импульс:

$mv_\alpha' = mv_{\alpha x} - F_{nep} \Delta t = mv_\alpha \cos{\alpha} - \mu \cdot \frac{mv_{\alpha y}}{\Delta t} \cdot \Delta t =$

$= mv_\alpha \cos{\alpha} - \mu mv_\alpha \sin{\alpha} = mv_\alpha ( \cos{\alpha} - \mu \sin{\alpha} )$ ;

$v_\alpha' = v_\alpha ( \cos{\alpha} - \mu \sin{\alpha} )$ ;

Из последнего вытекает очевидное условие, что:

$\cos{\alpha} - \mu \sin{\alpha} 0$ ;

$\cos{\alpha} \mu \sin{\alpha}$ ;

$\frac{\cos{\alpha}}{\sin{\alpha}} \mu$ ;

$tg{\alpha} < \frac{1}{\mu}$ , т.е. угол наклона должен быть не более определённого значения: $\alpha < arctg\frac{1}{\mu} = arcCtg{(\mu)}$ , иначе груз после удара о горизонтальную плоскость просто остановится, и никакого расстояния не пройдёт, а общая формула (данная в ответе) даст формально отрицательный ответ для высоты .

Кинетическая энергия груза после «ударного» торможения:

$E_{k\alpha}' = \frac{1}{2} mv_\alpha'^2 = \frac{1}{2} mv_\alpha^2 ( \cos{\alpha} - \mu \sin{\alpha} )^2$ ;

Далее, снова по закону сохранений энергии (с учётом неизменного значения потенциальной):

$E_{k\alpha}' - A_{ocm} = E_{k}'$ ;

где:

$A_{ocm} = F_{mp} \cdot s = \mu mg s$ – работа силы трения на горизонтальном участке до остановки;

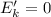а $E_{k}' = 0$ – конечная кинетическая энергия (остановка);

$\frac{1}{2} mv_\alpha^2 ( \cos{\alpha} - \mu \sin{\alpha} )^2 = \mu mg s$ ;

$\frac{v_\alpha^2}{2} = \frac{ \mu g s }{ ( \cos{\alpha} - \mu \sin{\alpha} )^2 }$ ;

Учитывая (*):

$gh ( 1 - \frac{\mu}{tg{\alpha}} ) = \frac{ \mu g s }{ ( \cos{\alpha} - \mu \sin{\alpha} )^2 }$ ;

$h ( 1 - \frac{\mu}{tg{\alpha}} ) = \frac{ \mu s }{ ( \cos{\alpha} - \mu \sin{\alpha} )^2 }$ ;

$h = \frac{ s }{ ( 1/ \mu - 1/ tg{\alpha} )( \cos{\alpha} - \mu \sin{\alpha} )^2 }$ .

*** Если же переход от наклонной плоскости гладкий, и при этом: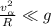 $\frac{v_\alpha^2}{R} \ll g$ , т.е. радиус перехода: 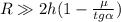$R \gg 2h ( 1 - \frac{\mu}{tg{\alpha}} )$ , то «ударная» потеря – пренебрежима, и: $v_\alpha' = v_\alpha$ , а, значит:

$h = \frac{ \mu s }{ 1 - \mu Ctg{(\alpha)} } = \frac{ s }{ 1/\mu - 1/tg{(\alpha)} }$ .

4,8(8 оценок)

Ответ:

Карина2000017

04.03.2021

№1 v2-v1 = 10 м/с

t = v2-v1 / a = 10 / 0.5 = 100 /5 =20 c

Hublle avatar

№2Данные задачи: t (продолжительность разгона данного автомобиля) = 10 с; V1 (приобретенная скорость) = 20 м/с; V2 (скорость, которую должен достичь данный автомобиль) = 108 км/ч (в СИ V2 = 30 м/с).

1) Ускорение, с которым двигался данный автомобиль: a = V1 / t = 20 / 10 = 2 м/с2.

2) Продолжительность разгона до 108 км/ч: t = (V2 - V1) / a = (30 - 20) / 2 = 10 / 2 = 5 с.

ответ: Данный автомобиль двигался с ускорением 2 м/с2; от 20 м/с до 108 км/ч автомобиль будет разгоняться 5 с.

Hublle avatar

№3 Дано:

S=500м

t=10с

а-?

Воспользуемся формулой: S=v0*t + at^2/2.

Т.к. тело двигалось из состояния покоя,то v0=0,тогда

S=at^2/2

500=а100/2