Question

и 6 задачу. можно только 5.
очень

Answer 1

5. 9 А

6.

Объяснение:

Пятый номер на силу ампера:

$F_{a} =BILsin\alpha$

Поскольку линии магнитной индукции перпендикулярны проводнику с током, то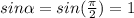 $sin\alpha =sin(\frac{\pi }{2} )=1$, следовательно:

$F_{a} =BILsin\alpha=BIL$

Найдём из этой формулы силу тока:

$I=\frac{F_{a} }{BL}=\frac{0.27}{30*10^{3} *1} =9 (A)$

Разберёмся с шестым.

Сила тока в витке:

$i=\frac{зq}{зt} = зq=i*зt$

По Закону Ома:

$i=\frac{E_{i} }{R}=-\frac{з(BScos\alpha )}{зt*R}$

подставим это в формулу для силы тока в витке:

$зq=i*зt=-\frac{з(BScos\alpha )}{зt*R}*зt=-\frac{з(BScos\alpha )}{R}=\frac{-B*S*(cos90-cos0)}{R} =0.0012$ (кулона)

Значит:

q1=0.0012 Кл=1.2 мКл

Если развернуть виток на 180 градусов, то по витку пройдёт в два раза больше заряда, поскольку сначала он повернётся на 90 градусов и ток будет идти в одну сторону, а когда виток будет поворачиваться c 90 градусов до 180 ток  пойдёт в другую сторону, то есть это будут два тока, одинаковые по модулю но разные по направлению:

q2=1.2*2=1.4 мКл

Вот и вся задача.