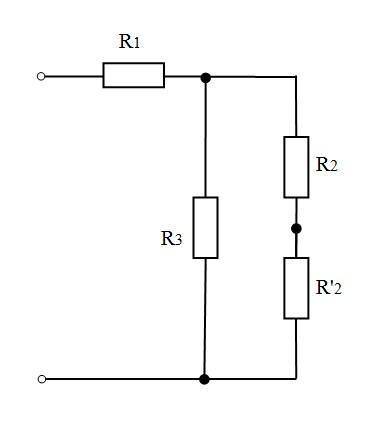
Схема состоит из:
группы сопротивлений R₂ и R₂', соединенных последовательно,
сопротивления R₃, соединенного параллельно с первой группой,
сопротивления R₁, соединенного последовательно с первыми двумя группами.
Преобразовать схему можно так: (см. рис.1)
Тогда общее сопротивление R₂ и R₂':
R₂₂ = R₂ + R₂' = 20 + 20 = 40 (Ом)
То есть сопротивления R₂ и R₂' можно заменить одним сопротивлением R₂₂ = 40 (Ом) (см. рис.2)
Общее сопротивление R₂₂ и R₃:
R₂₂₃ = R₂₂•R₃ : (R₂₂+R₃) = 40•60 : 100 = 24 (Ом)
Общее сопротивление цепи с учетом R₁:
R = R₁ + R₂₂₃ = 6 + 24 = 30 (Ом)
Общий ток в цепи:
I = I₁ = U/R = 240 : 30 = 8 (A)
Напряжение на первом сопротивлении:
U₁ = I · R₁ = 8 · 6 = 48 (B)
Напряжение на группе сопротивлений R₂₂₃:
U₂₂₃ = U - U₁ = 240 - 48 = 192 (B)
Ток, протекающий через R₃:
I₃ = U₂₂₃ : R₃ = 192 : 60 = 3,2 (A)
Ток, протекающий через R₂₂:
I₂₂ = U₂₂₃ : R₂₂ = 192 : 40 = 4,8 (A)
Напряжение на R₂ и R₂':
U₂ = U₂' = R₂I₂₂ = R₂'I₂₂ = 20 · 4,8 = 96 (B)
Теперь нам надо записать 2 закон Ньютона в векторном виде: →
→ → → → →
Fтяг+Fтр+mg+N=ma, теперь нам надо найти проекции этих сил на координатные оси ОХ: Fтяг-Fтр - mg sinα=ma (сила трения имеет отрицательную проекцию, тк. она направлена "против" оси ОХ, mg отрицательна т.к. идем от начала проекции к концу против направления оси, а если опустить перпендикуляр из конца вектора на ОХ то получим, что угол 30 будет лежать напротив проекции, т.е сам вектор при этом будет равен mg sinα)
Теперь аналогично находим проекции всех векторов на ОУ: 0+0-mg cosα+N=0 отсюда находим, что N=mg cosα, вспоминаем, что Fтр=μN=μ mg cosα, осталось все собрать в кучу, получаем: Fтяг- μ mg cosα - mg sinα=ma отсюда a=(Fтяг -μ mg cosα -mg sinα)/m=(7000-0,1*1000*10*√3/2 - 1000*10*1/2)/1000=(6150-5000)/1000=1150/1000=1,15 м/с.кв.