Question

Решить с дано кто может. 1) найдите период и частоту колебания, если маятник совершил 18 колебаний за 15 с. 2) найдите период колебаний маятника , если длина нити подвеса равна 40 см . здесь и ниже g=10м/с^2 3) каким будет период и частота колебаний маятника с длиной нити 10 м . 4) найдите длину нити маятника, совершающего 20 колебаний за 30 c.

Answer 1

Частота - это число колебаний в единицу времени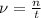 $\nu=\frac{n}{t}$, где n - число колебаний, t - промежуток времени (с). Вычислим: 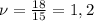$\nu=\frac{18}{15}=1,2$ Герц.

Период обратен частоте т.е.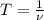 $T=\frac{1}{\nu}$. Вычислим: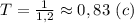 $T=\frac{1}{1,2}\approx0,83 \ (c)$

По формуле математического маятника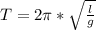 $T=2\pi*\sqrt{\frac{l}{g}}$, где l - длина маятника (м), g - ускорение свободного падения (g = 9,8 м/с² ≈ 10 м/с²). В системе СИ: 40 см = 0,4 метра. Подставляем числовые значения и вычисляем: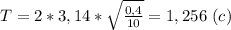 $T=2*3,14*\sqrt{\frac{0,4}{10}}=1,256 \ (c)$

По формуле математического маятника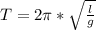 $T=2\pi*\sqrt{\frac{l}{g}}$, где l - длина маятника (м), g - ускорение свободного падения (g = 9,8 м/с² ≈ 10 м/с²). Подставляем и вычисляем: период: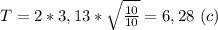 $T=2*3,13*\sqrt{\frac{10}{10}}=6,28 \ (c)$

Частота следовательно будет равна: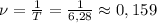 $\nu=\frac{1}{T}=\frac{1}{6,28}\approx0,159$ Гц

Используем две формулы периода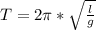 $T=2\pi*\sqrt{\frac{l}{g}}$, где l - длина маятника (м), g - ускорение свободного падения (g = 9,8 м/с² ≈ 10 м/с²) и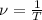 $\nu=\frac{1}{T}$

Левые части формул равны, следователь и правые части также равны: 

$\frac{1}{\nu}=2\pi*\sqrt{\frac{l}{g}}$.

Распишем частоту: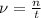 $\nu=\frac{n}{t}$

$\frac{1}{\frac{n}{t}}=2\pi*\sqrt{\frac{l}{g}}$

$\frac{t}{n}=2\pi*\sqrt{\frac{l}{g}}$

$n*2\pi*\sqrt{\frac{l}{g}}=t$

$(n*2\pi*\sqrt{\frac{l}{g}})^2=t^2$

$n^2*4\pi^2*\frac{l}{g}=t^2$

$l=\frac{g*t^2}{n^2*4\pi^2}$

Подставляем и вычисляем: 

$l=\frac{10*30^2}{20^2*4*3,14^2}\approx0,57 \ (_M)$