Дано:
T1= 1 секунда.
T2=1,1 cекунда.
a=?
_______
Из условия видно, что период увеличивается, следовательно лифт должен двигаться с ускорением, направленным вертикально вниз. (Данный факт следует из формул о весе тела, его движении вверх, или вниз с ускорением, так же, можно получить из второго закона Ньютона, расписывая силы, действущие на груз, который подвешен на математическом маятнике). ( длина маятника (l) - величина постоянная).
Запишем формулу периода математического маятника: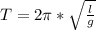
Теперь запишем данную формулу для двух случаев:

Возведем в квадрат и правую и левую часть каждого уравнения:
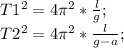
Поделим первое уравнение на второе:
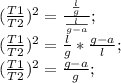
Теперь выведем ускорение (а):
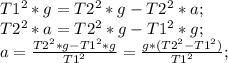
Посчитаем сначала периоды:
a=(g*(T2^2-T1^2)/(T1^2)=(g*(1,21-1)/(1,21)=0,17*g;
Подставляем значение ускорения свободного падения, равное, если быть более точным, 9,8 м/с^2.
a=0,17*9,8=1,666 м/с^2. Такое ускорение у лифтра. (если брать g=10м/с^2, то получим а=1,7 м/c^2).
ответ: а=1,666 м/с^2; (a=1,7 м/с^2).Лифт движется с ускорением, направленным вертикально вниз.
1.
Дано:
m=7 кг
V=300 км/ч
V₀=0
l=0.9 м
Найти: F-?
s= (V²-V₀²)/2a, т.к. V₀=0, то s=V²/(2a) - (домножим обе части на 2а, чтобы избавиться от знаменателя):
2as=V²
a=V²/(2s)
Теперь пользуясь формулой из второго закона Ньютона, подставим в него вместо ускорения a то, что у нас получилось:
F=m*a=m*V²/(2s) = (7*300²*1000²)/(3600²*2*0.9)=27006.17 Н= 27кН
ответ: F= 27кН
2.
А = Е2 - Е1
Е2 = mv²/2
E1 = mv₀²/2 + mgh
A = -18125 -2450h
3.
Дано:
m= 9.8 кг
Т = 3с
Найти:
k-?
v-?
1) Т = 2π√(m/k)
k = (4π²m)/T² = (4*9.8596*9.8)/9=49 Н/м
2) v = 1/T = 1/3 = 0.3 Гц
ответ: k=49 Н/м; v=0,3Гц
ослпдпдпдмзжсьвдп слпдпз