Имеем: g = 1,6 м/c²; T = 4,9 c. Найти: L - ?
1. Формула периода математического маятника: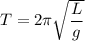 
.
2. Выразим длину: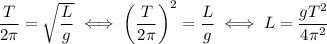 
.
3. Численно получим: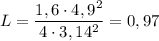 
(м).
Дано: C =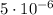 
Ф; T = 0,001 c. Найти: L - ?
1. Формула Томсона: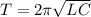 
.
2. Индуктивность из (1):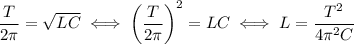 
.
3. Численно получим: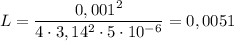 
(Гн).
4. Перевод: 0,0051 Гн = 5,1 мГн.
ответ: 5,1 мГн.======================Задача #3Имеем: x = 0,4cos(πt). Найти: A, T - ? Построить: x(t).
1. Уравнение гармонических колебаний в общем виде: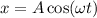 
, отсюда амплитуда A = 0,4 м и циклическая частота ω = π рад/с.
2. Формула циклической частоты: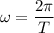 
, значит период: 
.
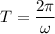3. Численно: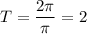 
(c).
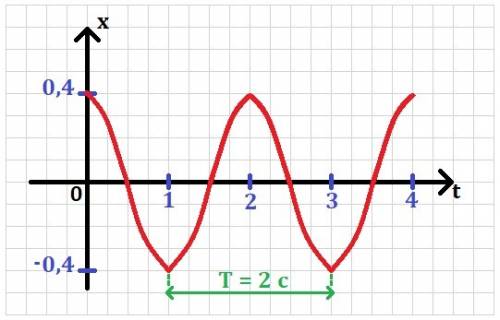
График зависимости x(t) смотри в приложении.
Мне так представляется, что ускорение мела (замедление, если угодно, отрицательное ускорение) в данной задаче постоянно.
Почему так?
Сила трения Fтр = N * mu = m * g * mu
Ускорение (как учил старина Ньютон) а = F / m.
В направлении движения, на мел действует единственная сила - трения, других я из условия не усматриваю.
Следовательно, ускорение
а = m * g * mu / m = g * mu = 10 * 0,3 = 3 м/с2
Обычное тело в таких условиях ехало бы путь
Х = v^2 / (2a) = 121 / 6 = 20,1666 м, но эх, какая незадача - мел истирается. Ок, так сколько же метров сможет вообще проехать мел до полной аннигиляции при условии заданных цифр?
х = 8 г / 0,5 г/м = 16 м. Жаль, недолог его путь. Но зато мы уже более близки к ответу.
Чисто технически мне проще сначала найти скорость u мела в момент его исчезновения.
х = ( v^2 - u^2 ) / (2a)
16 = (121 - u^2) / 6
u^2 = 25
u = 5 м/с - при этой скорости от мела, как от чеширского кота, остаётся лишь наглая глумливая ухмылка, и больше ничего.
Отсюда поищем время от начала движения до сего печального момента:
t = (v-u) / a = (11-5) / 3 = 2 c
Ну, может я ошибаюсь, но мне так кажется. Если, конечно, мел не украдут раньше в пути его следования.