1. Тело свободно падает с высоты 39,2 м. За какое время тело пройдет: а) первый метр своего пути; б) последний метр своего пути? Чему равна средняя скорость на второй половине пути?
Дано:
м
м/с²
Найти: а) б)
Решение. а) Следует определить время , за которое тело пройдет расстояние, равное м.
Направим ось в сторону падения тела. Воспользуемся формулой:
Перейдем от проекций к модулям:
Тогда
б) Время , за которое тело пройдет расстояние, равное
Полное время:
Тогда последний метр своего пути тело пройдет за:
Следует определить среднюю скорость на второй половине пути.
Длина первой половины пути –
Тогда можно записать, что , где – время прохождения телом первой половины пути, его можно найти:
Тогда время на второй половине пути:
Чтобы определить среднюю путевую скорость, нужно разделить весь путь на все время:
Определим значение искомых величин:
а)
б)
м/с
ответ: а) 0,45 с; б) 0,04 с; 24 м/с.
2. Тело, которое свободно падает без начальной скорости, за последнюю секунду движения проходит всего пути. Определите путь, пройденный телом за время падения.
Дано:
м/с²
Найти:
Решение. Высота падения тела:
Тогда путь где – путь, пройденный за время , то есть
Тогда
Имеем:
Сократим обе части уравнения на
Таким образом, тело весь путь за 2,37 с. Тогда
м
ответ: 28 м.
3. Тело свободно падает с высоты 60 м. Определите его перемещение за последнюю секунду падения.
Тут без чертежа никак: рисуем наклонную плоскость, на ней тело и расставляем силы: сила тяги вдоль наклонной плоскости вверх, сила трения вдоль плоскости, но вниз, сила тяжести приложена к центру масс тела и направлена ВЕРТИКАЛЬНО вниз, сила реакции опоры приложена к центру масс тела но ВДОЛЬ ПЕРПЕНДИКУЛЯРА К НАКЛОННОЙ ПЛОСКОСТИ. ось ОХ направляем вдоль наклонной плоскости вверх, ось ОУ вдоль вектора силы реакции опоры вверх, угол α=30 угол у основания наклонной плоскости. Теперь нам надо записать 2 закон Ньютона в векторном виде: → → → → → → Fтяг+Fтр+mg+N=ma, теперь нам надо найти проекции этих сил на координатные оси ОХ: Fтяг-Fтр - mg sinα=ma (сила трения имеет отрицательную проекцию, тк. она направлена "против" оси ОХ, mg отрицательна т.к. идем от начала проекции к концу против направления оси, а если опустить перпендикуляр из конца вектора на ОХ то получим, что угол 30 будет лежать напротив проекции, т.е сам вектор при этом будет равен mg sinα) Теперь аналогично находим проекции всех векторов на ОУ: 0+0-mg cosα+N=0 отсюда находим, что N=mg cosα, вспоминаем, что Fтр=μN=μ mg cosα, осталось все собрать в кучу, получаем: Fтяг- μ mg cosα - mg sinα=ma отсюда a=(Fтяг -μ mg cosα -mg sinα)/m=(7000-0,1*1000*10*√3/2 - 1000*10*1/2)/1000=(6150-5000)/1000=1150/1000=1,15 м/с.кв.
1. Тело свободно падает с высоты 39,2 м. За какое время тело пройдет: а) первый метр своего пути; б) последний метр своего пути? Чему равна средняя скорость на второй половине пути?
Дано:
Найти: а) б)
б) 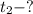
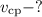
Решение. а) Следует определить время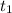 , за которое тело пройдет расстояние, равное
, за которое тело пройдет расстояние, равное 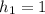 м.
м.
Направим ось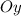 в сторону падения тела. Воспользуемся формулой:
в сторону падения тела. Воспользуемся формулой:
Перейдем от проекций к модулям:
Тогда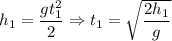
б) Время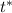 , за которое тело пройдет расстояние, равное
, за которое тело пройдет расстояние, равное 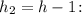
Полное время: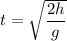
Тогда последний метр своего пути тело пройдет за: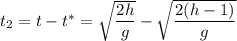
Следует определить среднюю скорость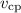 на второй половине пути.
на второй половине пути.
Длина первой половины пути –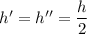
Тогда можно записать, что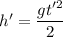 , где
, где 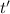 – время прохождения телом первой половины пути, его можно найти:
– время прохождения телом первой половины пути, его можно найти: 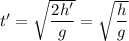
Тогда время на второй половине пути: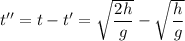
Чтобы определить среднюю путевую скорость, нужно разделить весь путь на все время:
Определим значение искомых величин:
а)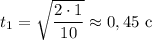
б)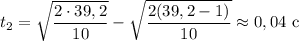
ответ: а) 0,45 с; б) 0,04 с; 24 м/с.
2. Тело, которое свободно падает без начальной скорости, за последнюю секунду движения проходит всего пути. Определите путь, пройденный телом за время падения.
всего пути. Определите путь, пройденный телом за время падения.
Дано:
Найти: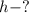
Решение. Высота падения тела: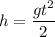
Тогда путь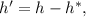 где
где 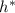 – путь, пройденный за время
– путь, пройденный за время  , то есть
, то есть 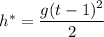
Тогда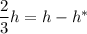
Имеем: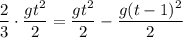
Сократим обе части уравнения на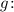
Таким образом, тело весь путь за 2,37 с. Тогда
ответ: 28 м.
3. Тело свободно падает с высоты 60 м. Определите его перемещение за последнюю секунду падения.
Дано:
Найти: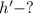
Решение. Полное время: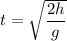
Пройденный путь тела за секунд:
секунд:
Имеем:
Определим значение искомой величины:
ответ: 30 м.