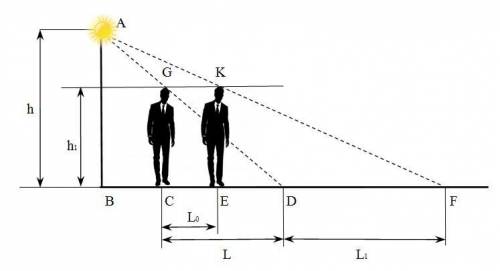
Дано: CD = 167 см; CG = h₁ = 186 см; CE = 42 см; EF = 251 см; ВС = х см.
Найти: AB = h
----------------------------------------------
Так как треугольники ABD и GCD подобны по первому признаку подобия (∠AВD = ∠GСD и ∠D - общий), то:
h/h₁ = BD/CD = (x + 167)/167
Треугольники ABF и KEF также подобны по двум углам. Тогда:
h/h₁ = BF/EF = (x + 42 + 251)/251
Найдем х = ВС:
(x + 167)/167 = (x + 42 + 251)/251
251x + 41917 = 167x + 48931
84x = 7014
x = 83,5 (см) => h/186 = (83,5 + 167)/167
167h = 46593
h = 279 (см)
ответ: 279 см.
V1*p1/T1=V*p/T0;V2*p2/T2=V*p/T0
Тогда V1*p1/T1=V2*p2/T2
Капля ртути будет перемещаться до тех пор, пока давление р1 не станет равным давлению р2, тогда имеем:
V1/T1=V2/T2
Но
V1 = V + S∙x, V2 = V – S∙x
(V +S∙х)*(T0 – ∆T) = (V – S∙х) *(Т0 + ∆T),
х — смещение капли ртути, S (200 кв.мм=2кв.см)— площадь сечения трубки,
тогда изменение объёма за счёт перемещения капли:
∆V = S∙x.
Тогда х равно
x = V∙∆T/(S∙T0)=200*2/(2*273)=0.73 см=7.3 мм.