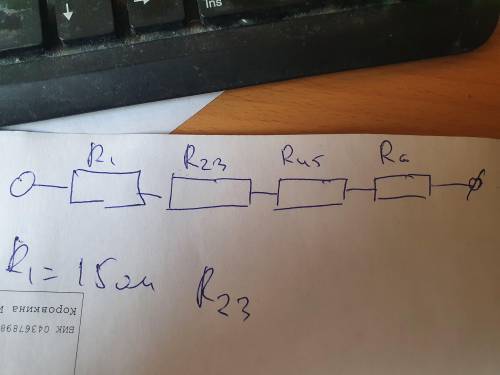
1) см рисунок
2) I₁ = I₆ = 50A
I₂ = 16.7 А
I₃ = 33.3 А
I₄ = 10 A
I₅ = 40 А
3) U₁ = 750 В
U₂ = U₃ = 166.5 B
U₄ = U₅ = 200 В
U₆ = 500 В
Объяснение:
1/R₂₃ = 1/R₂ + 1/R₃ = (R₂+R₃)/R₂R₃
R₂₃ = R₂R₃/(R₂+R₃)
R₄₅ = R₄R₅/(R₄+R₅)
R₂₃ = 50/15= 3,33 Ом
R₄₅ = 100/25 = 4 Ом
2. Струм
I₁ = I₂₃ = I₄₅ = I₆ = I
I = U/ (R₁ + R₂₃ + R₄₅ + R₆)
U = U₁ + U₂₃ + U₄₅+ U₆
U₂ = U₃
U₄ = U₅
I₅ = 40A
U₅ = R₅I₅ = 200 B
I₄ = U₅/R₄ = 200 В/20 Ом = 10 А
I = I₄₅ = I₁ = I₆ = 200 В / 4 = 50 А
U₂₃ = I*R₂₃ = 50А *3.33 Ом = 166,5 В
I₂ = U₂₃/R₂ = 166.5/10 = 16.7 А
I₃ = U₂₃/R₃ = 166.5/ 5 = 33.3 А
3. Напруга
U₁ = I₁*R₁ = 50A * 15Ом = 750 В
U₆ = I₆*R₆ = 50A * 10 Ом = 500 В
Остальные напруги из п. 2 берем посчитано уже.
ответ: h≈1,037 м.
Объяснение:
Пусть h и M - искомая толщина и масса льдины, а H - глубина водоёма. Пусть ρ1=900 кг/м³ - плотность льда, а ρ2=1000 кг/м³ - плотность воды. Пусть S=1 м² - площадь поверхности льдины, а Т=2 с - период колебаний льдины с человеком, масса которого m=80 кг. Возьмём координатную ось ОХ, совместим её начало О с дном водоёма и направим её вертикально вверх. Пусть x0 - координата нижнего края льдины до наступления на неё человеком. Так как в это время льдина плавает, то по второму закону Ньютона ρ2*S*(H-x0)*g-ρ1*S*h*g=0, где g≈10 м/с² - ускорение свободного падения. Пусть x- координата нижнего края льдины после наступления на неё человеком. По второму закону Ньютона, ρ2*S*(H-x)*g-(ρ1*S*h+m)*g=(ρ1*s*h+m)*d²x/dt². Оно приводится к виду d²x/dt²+x*ρ2*S*g/(ρ1*S*h+m)=(ρ2*S*x0*g-m*g)/(ρ1*S*h+m). Наконец, обозначая A=ρ2*S*g/(ρ1*S*h+m) и B=(ρ2*S*x0*g-m*g)/(ρ1*S*h+m), запишем это уравнение в виде x"+A*x=B. Это - неоднородное ЛДУ 2 порядка с постоянными коэффициентами, решение которого имеет вид: x=x1+x2, где x1 - общее решение однородного уравнения x1"+A*x1=0, а x2 - частное решение данного неоднородного уравнения. Для решения уравнения x1"+A*x1=0 составляем характеристическое уравнение (ХУ): k²+A=0. Так как A>0, то это уравнение имеет комплексные корни k1=i*√A и k2=-i*√A, где i=√(-1. Отсюда x1=C1*cos(t*√A)+C2*sin(t*√A)=C*sin(t*√A+α), где C1 и C2 - произвольные постоянные, C=√(C1²+C2²), α=arctg(C1/C2). Частное решение x2=B/A. Тогда x=x1+x2=C*sin(2*π*t/T+α)+B/A. Отсюда следует, что 2*π/T=√A, откуда A=ρ2*S*g/(ρ1*S*h+m)=4*π²/T² и h=ρ2*g*T²/(4*π²*ρ1)-m/(ρ1*S)≈1,037 м.