ТЕПЛОТА, кинетическая часть внутренней энергии вещества, определяемая интенсивным хаотическим движением молекул и атомов, из которых это вещество состоит. Мерой интенсивности движения молекул является температура. Количество теплоты, которым обладает тело при данной температуре, зависит от его массы; например, при одной и той же температуре в большой чашке с водой заключается больше теплоты, чем в маленькой, а в ведре с холодной водой его может быть больше, чем в чашке с горячей водой (хотя температура воды в ведре и ниже).
Мост Уитстона является сбалансированным когда разность потенциалов равна нулю, по нашей схеме если φ1-φ2=0, то мост Уитстона в нашем случае является сбалансированным.
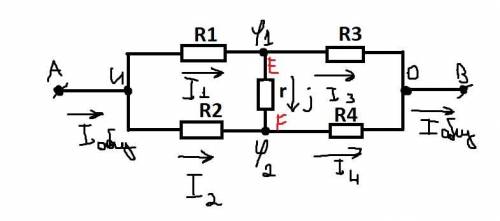
В узел E, поступает ток I1 и из узла выпускает ток I3 и j, ток j=0, так как напряжение - это разность потенциалов, а у нас в этом месте φ1-φ2=0 то есть как раз разность потенциалов равна нулю (так как это сбалансированный мост Уитстона) значит и напряжение на этом участке равно 0 и по закону Ома j=U/r где r-сопротивление резистора; j-ток протекающий через этот участок; U-разность потенциалов на этом участке. Следовательно j=0/r даже не зная r понятно, что j=0 А так как 0 в числителе. Поэтому по закону сохранения заряда какой ток поступает в узел такой и выпускает. То есть I1=I3+j мы выяснили что j=0, следовательно I1=I3.
В узел F, поступает ток j и I2, а выпускается ток I4. По закону сохранения заряда j+I2=I4 так как мы выяснили, что j=0, то I2=I4.
Так как φ1-φ2=0, то φ1=φ2 обозначим их как просто φ, то есть φ1=φ2=φ.
Так как напряжение - это разность потенциалов (по определению), то по закону Ома:
I1=(U-φ1)/R1=(U-φ)/R1
I3=(φ1-0)/R3=(φ-0)/R3=φ/R3
I2=(U-φ2)/R2=(U-φ)/R2
I4=(φ2-0)/R4=(φ-0)/R4=φ/R4
Раз I1=I3 и I2=I4, то:
1) I1=I3
(U-φ)/R1=φ/R3
2) I2=I4
(U-φ)/R2=φ/R4
Составим систему уравнений:
(U-φ)/R1=φ/R3
(U-φ)/R2=φ/R4
(U-φ)/φ=R1/R3
(U-φ)/φ=R2/R4
Следовательно:
R1/R3=R2/R4
R1*R4=R2*R3 - это значит, что когда у нас сбалансированный мост Уитстона, то произведения сопротивлений по диагонали равны.
Каждое равенство R1*R4=R2*R3 - это 1 комбинация (1 отдельный сбалансированный мост Уитстона), главное чтобы в каждой комбинации были разные R1 и R2 и R3 и R4 (так как по условию просят, чтобы резисторы, а следовательно и сопротивление было разным).
Также следим чтобы во всех комбинациях не повторялись цифры больше чем 5 раз, так как по условию у нас имеется по 5 штук резисторов каждого сопротивления от 1 Ом до 10 Ом.
Ну и само собой R1, R2, R3, R4 не может быть меньше 1 Ом и больше 10 Ом (по условию).
Я нашёл таких комбинаций 8 штук, вот они:
1) 1*10=2*5
2) 1*8=2*4
3) 1*6=2*3
4) 2*6=3*4
5) 2*10=4*5
6) 3*8=4*6
7) 3*10=5*6
8) 4*10=5*8
То есть итого можно собрать одновременно из этого набора как максимум 8 сбалансированных мостов Уитстона, при том что в каждой мостовой схеме все резисторы имеют разное сопротивление.
ответ: Можно собрать одновременно из этого набора как максимум 8 сбалансированных мостов Уитстона, при том что в каждой мостовой схеме все резисторы имеют разное сопротивление.Объяснение:
1)
3 мкВб = 3*10^(-6) Вб
70 мВ = 70*10^(-3) В = 7*10^(-2) В
ε = |dФ/dt| => dt = |dФ|/ε = 3*10^(-6) / 7*10^(-2) = 3*10^(-4) / 7 = 30*10^(-5) / 7 = 4,28571... * 10^(-5) = 4,3*10^(-5) = 43*10^(-6) = 43 мкс или 0,043 мс
2)
50 мОм = 50*10^(-3) Ом
6 мкВб = 6*10^(-6) Вб
I = |dq/dt|
ε = |dФ/dt|
I = ε/R => |dq/dt| = (|dФ/dt|) / R = |dФ|/dtR | * dt
|dq| = |dФ|/R = 6*10^(-6) / 50*10^(-3) = 6*10^(-6) / 5*10^(-2) = 6/5 * 10^(-4) = 1,2*10^(-4) = 120*10^(-6) = 120 мкКл или 0,12 мКл
3)
80 мГн = 80*10^(-3) Гн
0,05 с = 5*10^(-2) с
ε = L*|dI/dt| = 80*10^(-3) * 3/5*10^(-2) = 8*10^(-2) * 3/5^(-2) = 8*3/5 = 24/5 = 4,8 В
4)
0,5 с = 5*20^(-1) с
40 мВ = 40*10^(-3) В
ε = L*|dI/dt| => L = ε / |dI/dt| = ε *dt/|dI| = 40*10^(-3) * 5*10^(-1)/4 = 4*10^(-2) * 5*10^(-1)/4 = 5*10^(-3) = 5 мГн