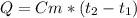Если направление тока в проводнике совпадает с направлением магнитного поля то магнитное поле на этот проводник.. допишите

👇

Увидеть ответ

Ответ:

ninazaripova1

15.01.2022

Не знаю хеххехезхехзех

4,6(96 оценок)

Открыть все ответы

Ответ:

Малефисента7

15.01.2022

Уравнение движения первого тела x1=-v0t+0.5at^2; a=g*sin(b), b- угол наклона плоскости.
для второго тела x2=v0t+0.5at^2;
Скорость первого тела равна: v1=x1'=-v0+at1; В момент остановки она равна нулю: v0=at1; Отсюда t1=v0/a;
Находим расстояния, пройденные телами за это время t1;
x1=-v0*v0/a+0.5a*v0^2/a^2;
x1=-v0^2/a+0.5v0^2/a;
x1=-0.5v0^2/a; (нас интересует отношение расстояний, поэтому берём модуль числа) x1=0.5v0^2/a;

x2=v0*v0/a+0.5a*v0^2/a^2;
x2=1.5v0^2/a;

x2/x1=(1.5v0^2/a)/(0.5v0^2/a);
x2/x1=3. Второе тело путь в три раза больше, чем первое.

4,4(18 оценок)

Ответ:

Eva5768

15.01.2022

Решения я не напишу. Скажу как такая задача должна решаться, дальше сама решишь, ибо хватит деградировать, учитесь решать простые задачи в конце концов
Задача будет состоять из 4-х действий
1. Нагревание. Для того чтобы нагреть 4кг льда от -30 до 0 градусов требуется теплота (до 0 градусов, потому что температура плавления/кристаллизации воды - 0 градусов. Всегда.). Найти её можно по формуле $Q=Cm*(t_{2}-t_{1})$ , где Q - теплота, С - удельная теплоёмкость (присутствует в учебнике. Ищи там и для воды, и для льда.), m - масса, 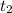$t_{2}$ - конечная температура, 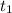$t_{1}$ - начальная температура.
2. Плавление. После того как лёд нагреется до 0-ой температуры, потребуется так же некоторое кол-во теплоты, чтобы лёд расплавился. Находится по формуле Q=λm, где Q - теплота, λ - удельная теплота плавления (опять же даётся в учебнике) и m - масса
3. Опять нагревание. После полного плавления льда, происходит нагревание воды от 0 до 100 градусов. Формула абсолютно та же самая что и в первом действии
4. Испарение. После нагревания воды, происходит такой процесс как конденсация - испарение. Формула Q=Lm, где Q - всё та же теплота, L - удельная теплота парообразования и m - масса.
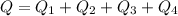После того как ты найдёшь Q в каждом действии, складываешь их: $Q= Q_{1} + Q_{2} + Q_{3} + Q_{4}$ , каждая Q обозначенная индексом является действием, которое ты делал, то бишь 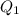$Q_{1}$ - Нагревание 1, а 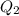$Q_{2}$ - плавление. Не перепутай.