1) Заметим, что какая бы ни была цепочка, если сопротивления всех ее звеньев увеличить вдвое, ее эквивалентное сопротивление также возрастет вдвое.
Заметим что наша цепочка это три последовательных резистора r, и паралелльно к ней присоединенная такая же бесконечная цепочка, но с удвоенным сопротивлением.
Поэтому
1/R = 1/(3r) + 1/(2R)
1/(2R) = 1/(3r)
R= 1.5 r
2) Откинем два крайних резистора пока
Обозначим ток, ушедший в первый горизонтальный резистор как A1, а ток ушедший в первый вертикальный резистор как B1, во второй горизонтальный A2, во второй вертикальный B2 и т д. Для любого звена с номером n имеем два правила Кирхгофа
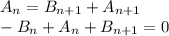
Отсюда
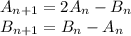
Пусть полный ток I в первом звене разделился как
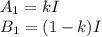
Посчитаем несколько первых звеньев по полученному правилу
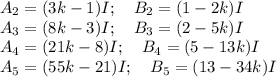
Заметим что коэффициенты при k в скобках и свободные члены это все числа Фибоначчи! Причем множитель при k это число Фибоначчи с номером на 2 большим, чем соответствующий свободный член.
При стремлении n к бесконечности, отношение коэффициента при k и свободного члена стремится к Ф^2, где число Ф = (1+√5)/2 - золотое сечение. Если k не будет равен 1/Ф^2, мы получим в итоге неограниченный рост токов при стремлении n к бесконечности, чего не может быть. Для компенсации растущих чисел Фибоначчи мы понимаем что k может быть только равен 1/Ф^2.
Теперь вспомним про два крайних резистора и посчитаем перепад напряжения от A к B идя по самому нижнему контуру (по последнему вертикальному резистору течет нулевой ток)
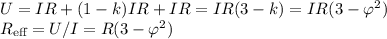
Где φ = 1/Ф = (1-√5)/2 ≈0.618
v = m/M (m - масса вещества, М - молярная масса вещества)
⇒ N = m/M × Na
M(воды) = 18г/моль
N(кол-во молекул в 200 г воды) = (200 × 10-³) ÷ (18 × 10-³) × 6,022 × 10²³ = 6.69 × 10^24 (10-³ - это десять в степени минус три, 10^24 - десять в двадцать четвёртой степени)
t = N/N1 (N1 - это число молекул, которые испаряются каждую секунду)
t = (6.69 × 10^24)/(5 × 10^19) = 1.338 × 10^5 = 133800 (c.)
Теперь считаем количество секунд в сутках: t1 = 24 × 60 × 60 = 86400 c.
t2 (время, за которое испарится весь стакан воды) = t ÷ t1 = 133800 ÷ 86400 = 1.548611 (сут.)
ответ: Вода испарится за ≈ 1.55 суток