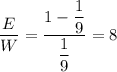Запишем уравнение гармонических колебаний в общем виде:
Будим считать, что маятник, в начальный момент времени, находился в положении максимального смещения от положения равновесия. В этом случае, когда мы отпустим маятник, он начнет совершать гармонические, незатухающие колебания.
Отсюда ⇒ (1)
Мы знаем, что потенциальную энергию пружинного маятника W, в любой момент времени t, можно вычислить как kx²(t)/2, а кинетическую энергию E, как mv²(t)/2.
То-есть , но согласно уравнению (1) получим
Аналогично , однако мы знаем, что
Тогда ⇒ , а это значит что
Поэтому , так как , то ⇒ (2)
Теперь определим cos²(ωt), мы знаем, что в нашем случае, в момент момент времени t растяжение пружины маятника составило А/3, тогда согласно уравнению (1) ⇒ , следовательно
M1-масса бензина, m2- масса воды, q-удельная теплота сгорания бензина с1-удельная теплоёмкость воды, с2-удельная теплоёмкость льда, t1- температура от -10 до 0 градусов, r1-удельная теплота плавления льда, r2-удельная теплота парообразования воды, t2-температура от 0 до 100 градусов
Энергия которая выделится при сгорании бензина пойдёт на нагрев, плавление льда, нагревание и парообразование воды. Энергия, которая выделится при сжигании бензина = m1*q Энергия, которая пойдёт на нагрев льда = m2*с2* t1 Энергия, которая пойдёт на топление льда = r1*m2 Энергия, которая пойдёт на нагрев воды = m2*c1*t2 Энергия, которая пойдёт на парообразование воды=r2*m2 Как я говорил, энергия, выделяющаяся при сжигании бензина пойдёт на все процессы, описанные выше. Значит: m1*q=(m2*c2*t1)+(r1*m2)+(m2*c1*t2)+(r2*m2) По условию нам нужно найти m1. Значит: m1=((m2*c2*t1)+(r1*m2)+(m2*c1*t2)+(r2*m2))/qКомментарии (3) Отметить нарушение
ответ: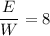
Объяснение:
Запишем уравнение гармонических колебаний в общем виде:
Будим считать, что маятник, в начальный момент времени, находился в положении максимального смещения от положения равновесия. В этом случае, когда мы отпустим маятник, он начнет совершать гармонические, незатухающие колебания.
Отсюда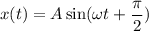
⇒ 
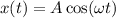(1)
Мы знаем, что потенциальную энергию пружинного маятника W, в любой момент времени t, можно вычислить как kx²(t)/2, а кинетическую энергию E, как mv²(t)/2.
То-есть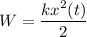
, но согласно уравнению (1) получим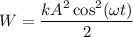 
Аналогично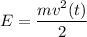
, однако мы знаем, что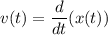 
Тогда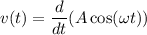
⇒ 
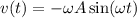, а это значит что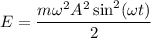 
Поэтому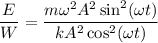
, так как 
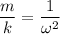, то 
⇒
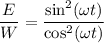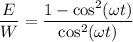(2)
Теперь определим cos²(ωt), мы знаем, что в нашем случае, в момент момент времени t растяжение пружины маятника составило А/3, тогда согласно уравнению (1)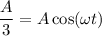
⇒ 
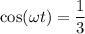, следовательно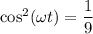 
Возвращаясь к уравнению (2) получим