Рассмотрим случай вращения твердого тела вокруг некоторой произвольной оси 00, (рис. 5.5). Вектор полного момента импульса L тела относительно неподвижной точки на оси вращения в общем случае не параллелен вектору угловой скорости о) и вычисляется согласно определению (4.36):
где ?j и V/ — радиус-вектор и скорость /-й частицы тела относительно полюса — некоторой точки О на рис. 5.5. Используем тот факт, что в системе координат, связанной с телом, составляющие вектора постоянны и скорость vi определяется как й,=1со,/*] согласно (2.20).
Тогда выражение (5.16) можно записать в виде
Отсюда проекция момента импульса на ось Xнеподвижной декартовой системы координат с началом в точке О определяется как линейная функция составляющих вектора угловой скорости со:
Аналогично вычисляются две другие проекции вектора L :
Введенные здесь девять коэффициентов 1тп (т, п — х, у, z) образуют квадратную матрицу, которая преобразуется как тензор второго порядка и называется тензором инерции (тензором момента инерции):
Диагональные компоненты тензора инерции — коэффициенты 7^, 7 , /_. — это моменты инерции тела относительно осей X, У и Z. Недиагональные компоненты тензора (5.17) называются центробежными моментами инерции тела. Поскольку / = 7 , Ixz = /,х и / = I , то тензор инерции является симметричным. В случае, когда масса т твердого тела непрерывно распределена по его объему, , 7 , Iопределяются по формулам (5.6а)—(5.6в). При этом центробежные моменты инерции будут определяться так:
Как известно, любой симметричный тензор или матрицу можно диаго- нализировать, т.е. для любого тела можно выбрать три такие взаимно перпендикулярные оси X, У, Z, для которых все недиагональные компоненты равны нулю и тензор инерции принимает вид
Такие оси являются главными осями инерции тела, а сохранившиеся диагональные компоненты тензора инерции — это главные моменты инерции. Тогда проекции момента импульса на главные оси инерции имеют вид
Как следует из полученных формул, даже в этом случае вектор Z не совпадает с вектором со по направлению.
Таким образом, тензор инерции любого тела зависит от точки, относительно которой он рассчитан. Когда ось вращения твердого тела закреплена и совпадает с одной из осей координат, например с осью Z, то вектор угловой скорости направлен по оси Z (соЛ. =cov, =0 и со. — со) и Т. = /„со=/со. Однако если ось вращения твердого тела не закреплена, то ее нельзя считать все время направленной вдоль фиксированной оси Z и необходимо вычислять все компоненты тензора инерции.
Объяснение:
Пройдя разность потенциалов 2 кВ, электрон влетает в однородное магнитное поле с индукцией 150 мкТл и движется по окружности радиусом 1 м. Определите по этим данным отношение заряда электрона к его массе.
Дано:
Δφ = 2 кВ = 2 000 В
B = 150 мкТл = 150·10⁻⁶ Тл
R = 1 м
____________________
e/m - ?
Работа электрического поля:
A = e·Δφ (1)
Кинетическая энергия электрона:
Eк = m·V²/2 (2)
Ларморовский радиус:
R = m·V / (e·B) (3)
Из (3) находим скорость электрона в магнитном поле:
V = e·B·R / m (4)
Подставляем (4) в (2):
Eк = m·V²/2 = m·e²·B²·R² / (2·m²) =
= e²·B²·R² / (2·m) (5)
Приравняем (5) и (1)
e²·B²·R² / (2·m) = e·Δφ
e·B²·R² / (2·m) = Δφ
(e/m) = 2·Δφ / (B²·R²)
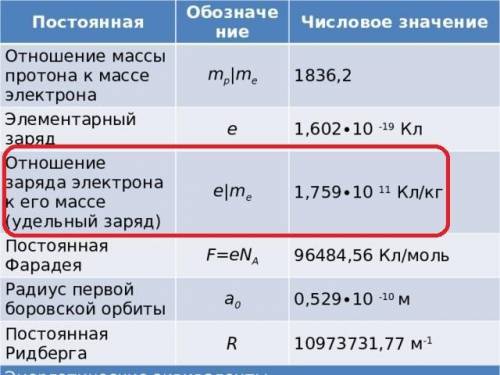
e/m = 2·2000 / (150·10⁻⁶)² = 1,78·10¹¹ Кл/кг
Замечание. Иногда полезно заглянуть в справочник. Задачу мы решили верно!
1)ОHKaMaAlKr4F5Su6
2) у Пермаганати