Дано:
m1 = 0,5 кг
m2 = 1 кг
α = 30°
μ = 0,2
g = 10 м/с²
а, Т - ?
а) Предполагается, что кабель не растягивается. Тогда ускорения грузов одинаковы:
а1 = а2 = а
Кроме того, "frictionless pulley" - блок без трения. Значит, его вес не учитывается. И значит силы, действующие на блок (а это силы натяжения кабеля Т1 и Т2), равны. Он просто меняет направление силы, действие которой передаётся кабелем от одного груза к другому (по Третьему закону Ньютона).
Укажем направление сил для каждого груза. Для первого груза ось Х направим параллельно плоскости и вправо, тогда ось Υ - перпендикулярно ей и вверх. Для второго груза используем только ось Υ и направим её вниз. На первый груз действуют сила трения Fтр (направлена против оси Х), сила тяжести m1g (направлена строго вниз, перпендикулярно поверхности, на которой расположена наклонная плоскость), сила реакции опоры N (направлена перпендикулярно плоскости) и сила натяжения кабеля Т1 (направлена параллельно плоскости вправо). На второй груз действуют сила натяжения нити Т2 (направлена вверх, против оси Y) и сила тяжести m2g (направлена вниз). Оба груза движутся с ускорением а. Тогда составим уравнения по Второму закону Ньютона, учитывая, что Т1 = Т2 = Т.
Для первого груза - в проекциях на оси:
ОХ: Т - Fтр - m1g*sinα = m1a
OY: N - m1g*cosα = 0 => N = m1g*cosα
Fтр = μN = μm1g*cosα => T - μm1g*cosα - m1g*sinα = m1a
Для второго груза:
ОY: m2g - T = m2a
Теперь выразим силу натяжения кабеля из каждого уравнения и приравняем выражения друг к другу:
Т = m1a + μm1g*cosα + m1g*sinα
Τ = m2g - m2a
m1a + μm1g*cosα + m1g*sinα = m2g - m2a
m1a + m2a = m2g - m1g*sinα - μm1g*cosα
a*(m1 + m2) = m2g - m1g*(sinα + μcosα)
a = (m2g - m1g*(sinα + μcosα)) : (m1 + m2) = (1*10 - 0,5*10*(sin30° + 0,2*cos30°)) : (0,5 + 1) = (10 - 5*(0,5 + 0,2*√3/2)) : 1,5 = 4,42... = 4,4 м/с²
б) Поделим первое уравнение на второе и выразим Т:
m1a/m2a = (T - μm1g*cosα - m1g*sinα) : (m2g - T)
m1*(m2g - T) = m2*(T - μm1g*cosα - m1g*sinα)
m1m2g - Tm1 = Tm2 - m2*μm1g*cosα - m2*m1g*sinα
Tm2 + Tm1 = m1m2g + m2*μm1g*cosα + m2*m1g*sinα
T*(m1 + m2) = m1m2g*(1 + μcosα + sinα)
Τ = m1m2g*(1 + μcosα + sinα)/(m1 + m2) = 0,5*1*10*(1 + 0,2*√3/2 + 0,5)/(0,5 + 1) = 5*(1,5 + 0,2*√3/2)/1,5 = 5,57... = 5,6 H
ответ: 4,4 м/с², 5,6 Н.
Дано:
q₁ = 2q
q₂ = q
q₃ = q
r₁₂ = r₂₁ = L
r₂₃ = r₃₂ = L
k
F, E, Wp - ?
Массив из трёх зарядов образует прямоугольный треугольник с равными катетами L (расстояниями r₁₂ и r₂₃). Тогда расстояние r₁₃ (гипотенуза) по правилу Пифагора равно:
r₁₃ = √(r₁₂² + r₂₃²) = √(L² + L²) = √(2L²) = √2*L =>
=> r₁₃ = r₃₁ = √2*L
Но нам будет удобен квадрат расстояния r₁₃(r₃₁):
r₁₃² = r₃₁² = 2L²
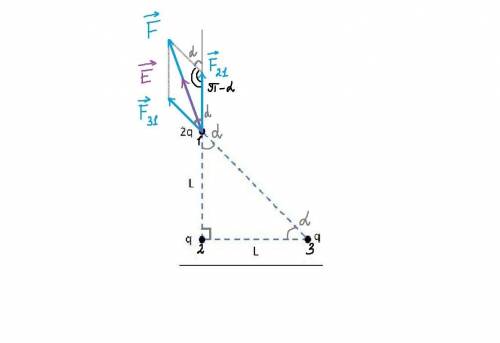
Т.к. две стороны треугольника равны, то треугольник является равнобедренным. Тогда углы при основании (r₁₃) равны. Т.к. угол в вершине треугольника (q₂) является прямым, т.е. 90°, то углы при основании равны α = 45°.
а) Теперь найдём силы, с которыми действуют на заряд q₁ заряды q₂ и q₃ (что то же самое - найдём "силу заряда, вызванную двумя другими зарядами"). Все заряды являются положительными, значит действующие между ними кулоновские силы - это силы отталкивания:
F₃₁ = k*(q₁*q₃)/r₃₁² = k*(2q*q)/(2L²) = k*q²/L²
F₂₁ = k*(q₁*q₂)/r₂₁² = k*(2q*q)/L² = k*2q²/L²
Чтобы найти F, надо найти векторную сумму (F₃₁ + F₂₁). Я опущу значок вектора в следующем выражении, но он должен быть над всеми F:
F = F₃₁ + F₂₁
А вот как эта сумма будет выглядеть геометрически (уже без значков):
F = √(F₃₁² + F₂₁² - F₃₁*F₂₁*cos(π - α)) - для нахождения F использована теорема косинусов. На рисунке показано, как получается угол (π - α). Угол между вектором F₂₁ и вектором F₃₁ равен углу α, т.к. этот угол и угол между гипотенузой треугольника и противолежащим катетом являются вертикальными. Угол между продолжением вектора F₂₁ и стороной параллелограмма, равной длине вектора F₃₁, равен углу α, т.к. он и угол между вектором F₂₁ и вектором F₃₁ являются соответственными. Ну а продолжение вектора силы F₂₁ составляет развёрнутый угол в 180° Т.е., π. Тогда угол между стороной параллелограмма, равной длине вектора F₂₁, и стороной параллелограмма, равной длине вектора F₃₁, равен разности развёрнутого угла π и угла α: (π - α). Решаем:
F = √(F₃₁² + F₂₁² - F₃₁*F₂₁*cos(π - α)) - возведём для удобства обе части уравнения в квадрат:
F² = F₃₁² + F₂₁² - F₃₁*F₂₁*cos(π - α) = F₃₁² + F₂₁² - F₃₁*F₂₁*(-cosα) = k²*q⁴/L⁴ + k²*2²q⁴/L⁴ + (k*q²/L²)*(k*2q²/L²)*cosα = k²*q⁴/L⁴ + k²*2²q⁴/L⁴ + cosα*k²*2q⁴/L⁴ = (k²*q⁴/L⁴)*(1 + 4 + 2cosα) = (k²*q⁴/L⁴)*(5 + 2cosα) =>
=> F = (k*q²/L²)*√(5 + 2cosα) - это и есть ответ.
б) Найти электрическое поле - значит найти его напряжённость Е. Напряжённость - это отношение силы Кулона, действующей на заряд, к самому заряду:
E = F/q
Мы уже вычислили результирующую силу, действующую на заряд q₁. Тогда напряжённость равна:
E = F/q₁ = ((k*q²/L²)*√(5 + 2cosα)) : 2q = (k*q²/L²)*(1/2q)*√(5 + 2cosα) =>
=> E = (1/2)*(k*q/L²)*√(5 + 2cosα)


при одинаковом g 3500г/700г=5 раз