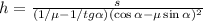 , при условии:
, при условии: 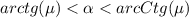 ;
;
*** если же переход от наклонной плоскости скруглённый, и: 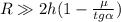 , то:
, то:
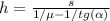 .
.
Объяснение:
По закону сохранений энергии:
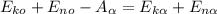 ;
;
где:
 и
и 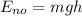 – начальные значения кинетической и потенциальной энергии;
– начальные значения кинетической и потенциальной энергии;
 и
и 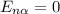 – значения кинетической и потенциальной энергии перед ударом о горизонтальную поверхность, в самом низу наклонной плоскости;
– значения кинетической и потенциальной энергии перед ударом о горизонтальную поверхность, в самом низу наклонной плоскости;
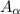 – работа силы трения на наклонной плоскости;
– работа силы трения на наклонной плоскости;
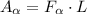 – работа
– работа
силы трения 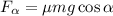 на наклонной плоскости,
на наклонной плоскости,
где: 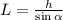 – длина наклонной плоскости;
– длина наклонной плоскости;
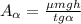 ;
;
В итоге:
 ;
;
(*) 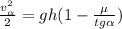 ;
;
Из этого вытекает очевидное условие, что:
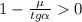 ;
;
 ;
;
 , т.е. угол наклона должен быть более значения:
, т.е. угол наклона должен быть более значения: 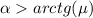 , иначе груз вообще не сдвинется с места, и, разумеется, никакого расстояния
, иначе груз вообще не сдвинется с места, и, разумеется, никакого расстояния  не пройдёт, а общая формула (данная в ответе) даст формально отрицательный ответ для высоты
не пройдёт, а общая формула (данная в ответе) даст формально отрицательный ответ для высоты 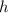 .
.
Теперь «удар», т.е. переход с наклонной плоскости на горизонталь. Во время удара теряется вертикальная составляющая импульса 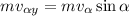 . Это происходит почти мгновенно (
. Это происходит почти мгновенно ( 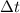 ), под воздействием гасящей его чрезвычайно резко возрастающей на время гашения силы реакции опоры (и веса – соответственно)
), под воздействием гасящей его чрезвычайно резко возрастающей на время гашения силы реакции опоры (и веса – соответственно) 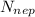 . Удар груза об опору в момент его перехода на горизонталь будем считать абсолютно неупругим, происходящим таким образом, что груз после него не подскакивает. Тогда можно записать, что:
. Удар груза об опору в момент его перехода на горизонталь будем считать абсолютно неупругим, происходящим таким образом, что груз после него не подскакивает. Тогда можно записать, что:
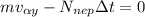 ;
;
 ;
;
За это время 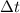 груз так же заметно замедляется под воздействием чрезвычайно резко возрастающей на время гашения силы трения:
груз так же заметно замедляется под воздействием чрезвычайно резко возрастающей на время гашения силы трения:
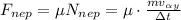 ;
;
Соответственно, гасится и горизонтальный импульс:

 ;
;
 ;
;
Из последнего вытекает очевидное условие, что:
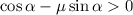 ;
;
 ;
;
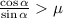 ;
;
 , т.е. угол наклона должен быть не более определённого значения:
, т.е. угол наклона должен быть не более определённого значения: 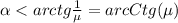 , иначе груз после удара о горизонтальную плоскость просто остановится, и никакого расстояния
, иначе груз после удара о горизонтальную плоскость просто остановится, и никакого расстояния  не пройдёт, а общая формула (данная в ответе) даст формально отрицательный ответ для высоты
не пройдёт, а общая формула (данная в ответе) даст формально отрицательный ответ для высоты 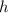 .
.
Кинетическая энергия груза после «ударного» торможения:
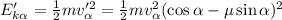 ;
;
Далее, снова по закону сохранений энергии (с учётом неизменного значения потенциальной):
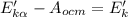 ;
;
где:
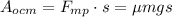 – работа силы трения на горизонтальном участке до остановки;
– работа силы трения на горизонтальном участке до остановки;
а 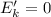 – конечная кинетическая энергия (остановка);
– конечная кинетическая энергия (остановка);
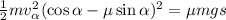 ;
;
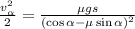 ;
;
Учитывая (*):
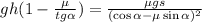 ;
;
 ;
;
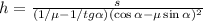 .
.
*** Если же переход от наклонной плоскости гладкий, и при этом: 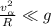 , т.е. радиус перехода:
, т.е. радиус перехода: 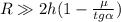 , то «ударная» потеря – пренебрежима, и:
, то «ударная» потеря – пренебрежима, и:  , а, значит:
, а, значит:
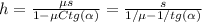 .
.
Объяснение:
1)
Пусть груз положили на правый (второй) груз.
Тогда:
m₁ = M
m₂ = M+Δm
Ускорение грузов вычислим по формуле (см. Физика-9, Кикоин):
a = g·(m₂ - m₁) / (m₁ + m₂)
a = g·(M + Δm -M) / (M + Δm + M) = g·Δm / (2·M + Δm)
a = 10·0,070 / (2·2+0,070) ≈ 0,17 м/с²
2)
Рассмотрим левый груз. Он движется вверх с ускорением a, тогда его вес:
P₁ = M·(g + a) = 2·(9,81 + 0,17) ≈ 19,96 Н
Для правого:
P₂ = (M+Δm)·(g + a) = (2+0,070)·(9,81 - 0,17) ≈ 19,96 Н
Вес - это сила, которая растягивает нить.
Значит, сила натяжения T = P₁ = P₂ = 19,96 Н