коэффициент трансформации >1
значит трансформатор является понижающим.
Напряжение на вторичной обмоткеЛучи, проходящие через центр линзы не отклоняются. Параллельные лучи собираются в точку в фокальной плоскости.
U2 = U1 / k = 120 B / 20 = 6 B.
Число витков во вторичной обмотке
Пусть угол падения А, угол преломления В, причём sinA=n*sinB. Пусть коэфф. преломления равен n, толщина пластины d. После выхода из пластины луч снова будет иметь угол А, однако он сместится на расстояние а.
Поскольку рисовать здесь я не умею, равно как и импортировать формулы, то могу тут лишь привести результат решения тригонометрической задачи
a=d*sinA*{1-cosA/sqrt[n^2-(sinA)^2]}
n2 = n1 / k = 200 / 20 = 10.
формулы ЭДС индукции в движущихся проводниках ЭДС=В*L*v*sin a
Дано:(запишем сразу все в СИ)
m1=0,200кг
m2=0,003кг
t1=20*С
t2=10*C
λ=335000Дж/кг
c=4200 Дж/кг*C⁰
1. Запишем уравнение теплового баланса в общем виде Q1+Q2+Q3...Qn=0, где Q- количество теплоты полученное телами.
2.В нашей задаче фигурируют Q-таяние снега и Q-охлаждения воды, тогда уравнение теплового баланса будет выглядеть следующим образом
Q(таяние снега)+Q(охлаждения воды)=0 отсюда
Q(таяние снега)=-Q(охлаждения воды), так как вода охлаждается, то её Q(полученное) будет равно -Q(охлаждения воды), то есть Q(охлаждения воды)=-Q(полученное) и Q(таяние снега)=-Q(полученное)тогда конечное уравнение теплового баланса будет иметь вид
-Q(таяние снега)=-(-Q)(охлаждения воды)⇒
Q(таяния снега)=-Q(охлаждения воды)-уравнение(1)
3. Q(таяние снега)=λm, где λ-удельная теплота снега, а m- масса растаявшего снега.
Q(охлаждения воды)=m1cΔt, где m1-масса воды, c-удельная теплоемкость воды, Δt-разница между конечной и начальной температурой, тогда из уравнения(1) λm=cm1Δt отсюда выразим массу растаявшего снега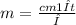 
, подставляем числа 
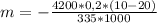≈0,025 кг
4. масса всей воды будет равна сумме предыдущий массы и растаявшего снега⇒ 0.2кг+0,025кг=0,225кг.
ответ: 0,225кг
ускорение будет равно F=ma где F 'это общая сила. Состоящая из F*cos(a)- (mg-mgsin(a))*коэфф.трения=ma все подставь, получишь a ускорение