Пусть - напряжённость электростатического поля создаваемым точечным зарядом . В некоторую точку этого электростатического поля помещают пробный заряд
По определению
Где - сила электростатического взаимодействия между двумя точечными зарядами и
Согласно закону Кулона
Где - расстояние между точечными зарядами и
Преобразуем первую формулу
Как видно из итоговой формулы напряженность электростатического поля создаваемым точечным зарядом никак не зависит от значения модуля пробного заряда внесенного в это поле.
В принципе формулу можно было записать и самого начала и объяснить что так и так. Или даже вовсе не записывать и все объяснить словами.
Во-первых, нужно уметь изображать силы, действующие на тело. Не умеешь этого - не решишь задачу.
1) У нас по условию дано "небольшое тело". Пусть это - какой-нибудь квадрат (можно и быть оригинальнее, но преподаватель едва ли оценит).
Разумеется, на него действует сила тяжести mg и сила нормальной реакции опоры N.
Так как он движется, то на него действует и сила трения Fтр, направленная противоположно силе тяги Fтяг.
Собственно, все. Рассмотрим первый случай.
Наш квадрат движется равномерно, следовательно, с постоянной скоростью (почитай про принцип относительности Галилея).
Работает первый закон Ньютона - равнодействующая всех сил, действующих на квадрат, равна нулю (не забываем, что сила - это вектор и его нужно проецировать, чтобы посчитать):
Fтяг + N + mg + Fтр = 0.
с N, mg и Fтр все хорошо, а вот Fтяг нужно проецировать, причем на обе оси.
Для ОХ: Fтяг(x) = Fтяг * cosα Для OY: Fтяг(y) = Fтяг * sinα
Теперь проецируем все силы на оси ОX и OY.
OY: Fтяг sinα + N - mg = 0 => N = mg - Fтяг sinα OX: Fтяг cosα - u N = 0,
Fтяг cosα = u (mg - Fтяг sinα) =>
u = Fтяг cosα / (mg - Fтяг sinα)
Знаем коэф-т трения. Круто. Теперь можем найти ускорение исходя из второго случая.
2) Все делаем аналогично. Единственное, что изменилось - работает второй закон Ньютона (равнодействующая всех сил равна ma).
ответ: Никак не измениться
Объяснение:
Пусть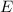
- напряжённость электростатического поля создаваемым точечным зарядом 
. В некоторую точку этого электростатического поля помещают пробный заряд 
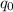
По определению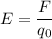
Где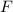
- сила электростатического взаимодействия между двумя точечными зарядами 
и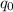 
Согласно закону Кулона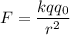
Где
- расстояние между точечными зарядами 
и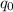 
Преобразуем первую формулу
Как видно из итоговой формулы напряженность электростатического поля создаваемым точечным зарядом
никак не зависит от значения модуля пробного заряда внесенного в это поле.
В принципе формулу
можно было записать и самого начала и объяснить что так и так. Или даже вовсе не записывать и все объяснить словами.